题目内容
设动点M(x,y)到直线y=3的距离与它到点F(0,1)的距离之比为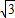 ,点M的轨迹为曲线E.
,点M的轨迹为曲线E.(I)求曲线E的方程:
(II)过点F作直线l与曲线E交于A,B两点,且
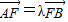 .当2≤λ≤3时,求直线l斜率k的取值范围•
.当2≤λ≤3时,求直线l斜率k的取值范围•
【答案】分析:(Ⅰ)利用动点M(x,y)到直线y=3的距离与它到点F(0,1)的距离之比为 ,建立方程,可得曲线E的方程;
,建立方程,可得曲线E的方程;
(Ⅱ)直线l方程为y=kx+1,代入曲线E方程,利用韦达定理及向量知识,可求直线l斜率k的取值范围.
解答:解:(Ⅰ)根据题意,∵动点M(x,y)到直线y=3的距离与它到点F(0,1)的距离之比为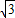 ,
,
∴|y-3|= •
•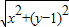 .
.
化简,得曲线E的方程为3x2+2y2=6.…(4分)
(Ⅱ)直线l方程为y=kx+1,代入曲线E方程,得(2k2+3)x2+4kx-4=0.…(6分)
设A(x1,y1),B(x2,y2),则x1+x2=-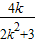 ,①x1x2=-
,①x1x2=-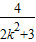 .②
.②
∵ =λ
=λ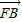 ,∴(-x1,1-y1)=λ(x2,y2-1),
,∴(-x1,1-y1)=λ(x2,y2-1),
由此得x1=-λx2.③
由①②③,得 +
+ =
= =
=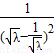 .…(9分)
.…(9分)
因为2≤λ≤3,所以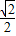 ≤
≤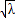 -
- ≤
≤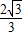 ,从而
,从而 ≤
≤ ≤2,
≤2,
解不等式 ≤
≤ +
+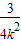 ≤2,得
≤2,得 ≤k2≤3.
≤k2≤3.
故k的取值范围是[- ,-
,- ]∪[
]∪[ ,
,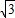 ].…(12分)
].…(12分)
点评:本题考查轨迹方程,考查向量知识的运用,考查直线与曲线的位置关系,考查韦达定理的运用,属于中档题.
 ,建立方程,可得曲线E的方程;
,建立方程,可得曲线E的方程;(Ⅱ)直线l方程为y=kx+1,代入曲线E方程,利用韦达定理及向量知识,可求直线l斜率k的取值范围.
解答:解:(Ⅰ)根据题意,∵动点M(x,y)到直线y=3的距离与它到点F(0,1)的距离之比为
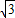 ,
,∴|y-3|=
 •
•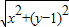 .
.化简,得曲线E的方程为3x2+2y2=6.…(4分)
(Ⅱ)直线l方程为y=kx+1,代入曲线E方程,得(2k2+3)x2+4kx-4=0.…(6分)
设A(x1,y1),B(x2,y2),则x1+x2=-
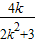 ,①x1x2=-
,①x1x2=-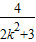 .②
.②∵
 =λ
=λ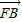 ,∴(-x1,1-y1)=λ(x2,y2-1),
,∴(-x1,1-y1)=λ(x2,y2-1),由此得x1=-λx2.③
由①②③,得
 +
+ =
= =
=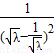 .…(9分)
.…(9分)因为2≤λ≤3,所以
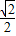 ≤
≤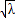 -
- ≤
≤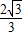 ,从而
,从而 ≤
≤ ≤2,
≤2,解不等式
 ≤
≤ +
+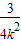 ≤2,得
≤2,得 ≤k2≤3.
≤k2≤3.故k的取值范围是[-
 ,-
,- ]∪[
]∪[ ,
,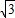 ].…(12分)
].…(12分)点评:本题考查轨迹方程,考查向量知识的运用,考查直线与曲线的位置关系,考查韦达定理的运用,属于中档题.

练习册系列答案
相关题目
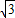 ,点M的轨迹为曲线E.
,点M的轨迹为曲线E.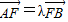 .当2≤λ≤3时,求直线l斜率k的取值范围•
.当2≤λ≤3时,求直线l斜率k的取值范围•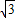 ,点M的轨迹为曲线E.
,点M的轨迹为曲线E.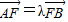 .当2≤λ≤3时,求直线l斜率k的取值范围•
.当2≤λ≤3时,求直线l斜率k的取值范围• ,点M的轨迹为曲线E.
,点M的轨迹为曲线E.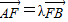 .当2≤λ≤3时,求直线l斜率k的取值范围•
.当2≤λ≤3时,求直线l斜率k的取值范围•