Question

在△ABC中角A，B，C对应边分别为a，b，c，若，那么c=________．

Answer 1

分析：利用已知的等式可得到 =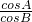，再由正弦定理得到 =，能得出 A=B，a=b，把 =+ 两边平方，且利用 •=-1，可得所求．
解答：由题意得 •=cb×cosA=1，•BC=ca×cosB=1，
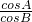∴=，再由正弦定理得 =，
∴sinAcosB=cosAsinB，
∴A=B，a=b．
又∵=+，
∴=b²=c²+a²+2 •=c²+b²-2，
∴c²=2，
∴c=，
故答案为 ．
点评：本题考查两个向量的数量积公式的应用，正弦定理的应用以及向量的分解．