题目内容
如图,棱锥P—ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD= .
.
(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)求二面角P—CD—B的大小;
(Ⅲ)求点C到平面PBD的距离. 
证:(Ⅰ)在Rt△BAD中,AD=2,BD= ,
,
∴AB=2,ABCD为正方形,因此BD⊥AC. …………2分
∵PA⊥平面ABCD,BDÌ平面ABCD,∴BD⊥PA .
又∵PA∩AC=A∴BD⊥平面PAC. …………4分
解:(Ⅱ)由PA⊥面ABCD,知AD为PD在平面ABCD的射影,又CD⊥AD,
∴CD⊥PD,知∠PDA为二面角P—CD—B的平面角. ……………6分
又∵PA=AD,∴∠PDA=450 . 二面角P—CD—B的大小是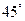 ……………8分
……………8分
(Ⅲ)∵PA=AB=AD=2∴PB=PD=BD=
设C到面PBD的距离为d,由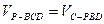 ,…………10分
,…………10分
有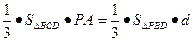 ,
,
即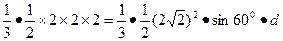 ,得
,得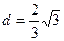 ………14分
………14分
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图三棱锥P-ABC中,平面PAB⊥平面ABC,AC⊥BC,BC=
如图三棱锥P-ABC中,平面PAB⊥平面ABC,AC⊥BC,BC= 如图三棱锥P-ABC中,△ABC是正三角形,∠PCA=90°,D为PA的中点,二面角P-AC-B为120°,PC=2,AB=
如图三棱锥P-ABC中,△ABC是正三角形,∠PCA=90°,D为PA的中点,二面角P-AC-B为120°,PC=2,AB= 如图三棱锥P-ABC,已知PC⊥平面ABC,CD⊥面PAB,BA=BC,PC=AC=2.
如图三棱锥P-ABC,已知PC⊥平面ABC,CD⊥面PAB,BA=BC,PC=AC=2. 如图三棱锥P-ABC中,△PAC,△ABC是等边三角形.
如图三棱锥P-ABC中,△PAC,△ABC是等边三角形.