题目内容
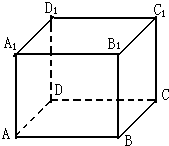 在正四棱柱ABCD-A1B1C1D1中,如果底边正方形ABCD的边长为AB=2,侧棱AA1=
在正四棱柱ABCD-A1B1C1D1中,如果底边正方形ABCD的边长为AB=2,侧棱AA1=| 2 |
①AA1与BC1成45°角;
②AA1与BC1的距离为2;
③二面角C1-AB-C为arctan
| ||
| 2 |
④B1D⊥平面D1AC.
则正确命题的序号为
②③
②③
.分析:①由题意可得:BC1∥AD1,所以AA1与BC1成的角等于AA1与AD1成的角.再根据AB=2,侧棱AA1=
,可得AA1与BC1成不等于45°角.
②由题意可得:线段AB是AA1与BC1的公垂线,可得AA1与BC1的距离为线段AB的长度.
③连接BC1,根据题意与二面角平面角的定义可得∠C1BC是二面角C1-AB-C的平面角,再利用解三角形的有关知识求出答案.
④连接AD1,A1D,由题中条件可得:AD1与A1D不垂直,进而得到B1D与AD1不垂直,可得B1D与平面D1AC不垂直.
| 2 |
②由题意可得:线段AB是AA1与BC1的公垂线,可得AA1与BC1的距离为线段AB的长度.
③连接BC1,根据题意与二面角平面角的定义可得∠C1BC是二面角C1-AB-C的平面角,再利用解三角形的有关知识求出答案.
④连接AD1,A1D,由题中条件可得:AD1与A1D不垂直,进而得到B1D与AD1不垂直,可得B1D与平面D1AC不垂直.
解答:解:①由题意可得:ABCD-A1B1C1D1是正四棱柱,所以BC1∥AD1,所以AA1与BC1成的角等于AA1与AD1成的角.
又因为正方形ABCD的边长为AB=2,侧棱AA1=
,
所以AA1与BC1成不等于45°角,所以①错误.
②由正四棱柱ABCD-A1B1C1D1的结构特征可得:线段AB是AA1与BC1的公垂线,所以AA1与BC1的距离为线段AB的长度,所以AA1与BC1的距离为2,所以②正确.
③连接BC1,由正四棱柱的结构特征可得AB⊥BC1,AB⊥BC,所以根据二面角平面角的定义可得∠C1BC是二面角C1-AB-C的平面角.
因为正方形ABCD的边长为AB=2,侧棱AA1=
,
所以tan∠C1BC=
=
,所以二面角C1-AB-C为arctan
,所以③正确.
④连接AD1,A1D,因为正方形ABCD的边长为AB=2,侧棱AA1=
,所以AD1与A1D不垂直,所以根据三垂线定理可得B1D与AD1不垂直,所以B1D与平面D1AC不垂直,所以④错误.
故答案为:②③
又因为正方形ABCD的边长为AB=2,侧棱AA1=
| 2 |
所以AA1与BC1成不等于45°角,所以①错误.
②由正四棱柱ABCD-A1B1C1D1的结构特征可得:线段AB是AA1与BC1的公垂线,所以AA1与BC1的距离为线段AB的长度,所以AA1与BC1的距离为2,所以②正确.
③连接BC1,由正四棱柱的结构特征可得AB⊥BC1,AB⊥BC,所以根据二面角平面角的定义可得∠C1BC是二面角C1-AB-C的平面角.
因为正方形ABCD的边长为AB=2,侧棱AA1=
| 2 |
所以tan∠C1BC=
| CC1 |
| BC |
| ||
| 2 |
| ||
| 2 |
④连接AD1,A1D,因为正方形ABCD的边长为AB=2,侧棱AA1=
| 2 |
故答案为:②③
点评:此题主要考查线面垂直的判断定理与异面直线的距离,以及考查线线角与二面角的有关知识,解决异面直线的距离问题的关键是找出两条异面直线的公垂线,而解决空间角的关键是找出空间角,其步骤是:作角,证角,求角,此题综合性较强考查的问题很基础,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在正四棱柱ABCD-A1B1C1D1中,棱长AA1=2,AB=1,E是AA1的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,棱长AA1=2,AB=1,E是AA1的中点. 在正四棱柱ABCD-A1B1C1D1中,AA1=2AB,E为CC1的中点.
在正四棱柱ABCD-A1B1C1D1中,AA1=2AB,E为CC1的中点. 如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,M、N分别为B1B和A1D的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,M、N分别为B1B和A1D的中点.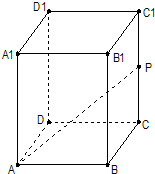 (2012•长宁区一模)在正四棱柱ABCD-A1B1C1D1中,已知底面ABCD的边长为2,点P是CC1的中点,直线AP与平面BCC1B1成30°角,求异面直线BC1和AP所成角的大小.(结果用反三角函数值表示)
(2012•长宁区一模)在正四棱柱ABCD-A1B1C1D1中,已知底面ABCD的边长为2,点P是CC1的中点,直线AP与平面BCC1B1成30°角,求异面直线BC1和AP所成角的大小.(结果用反三角函数值表示)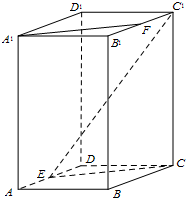 (2012•昌平区二模)在正四棱柱ABCD-A1B1C1D1中,E为AD中点,F为B1C1中点.
(2012•昌平区二模)在正四棱柱ABCD-A1B1C1D1中,E为AD中点,F为B1C1中点.