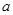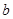题目内容
(某品牌的汽车4S店,对最近100位采用分期付款的购车者进行统计,统计结果如下表所示:已知分3期付款的频率为0.2,4S店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元,分2期或3期付款其利润为1.5万元;分4期或5期付款,其利润为2万元,用η表示经销一辆汽车的利润.
(Ⅰ)求上表中的a,b值;
(Ⅱ)若以频率作为概率,求事件A:“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的频率P(A);
(Ⅲ)求η的分布列及数学期望Eη.
| 付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
| 频数 | 40 | 20 | a | 10 | b |
(Ⅱ)若以频率作为概率,求事件A:“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的频率P(A);
(Ⅲ)求η的分布列及数学期望Eη.
分析:(I)根据分3期付款的频率为0.2,以及频数=样本容量×频率,可求出a的值,再根据总数为100可求出b的值;
(II)购买该品牌汽车的3为顾客中至多有1位采用3期付款有两种情形,一种情况是没有人采用3期付款,一种情况是只有1人采用3期付款,分别求出相应的概率,求和即可;
(III)根据η的可能取值为1,1.5,2,然后分别求出相应的概率,列出分布列,最后利用数学期望公式解之即可.
(II)购买该品牌汽车的3为顾客中至多有1位采用3期付款有两种情形,一种情况是没有人采用3期付款,一种情况是只有1人采用3期付款,分别求出相应的概率,求和即可;
(III)根据η的可能取值为1,1.5,2,然后分别求出相应的概率,列出分布列,最后利用数学期望公式解之即可.
解答:解:(Ⅰ)由
=0.2,可得a=20,∴b=100-40-20-20-10=10
(Ⅱ)记分期付款的期数为ξ,依题意得
P(ξ=1)=0.4,P(ξ=2)=0.2,P(ξ=3)=0.2,P(ξ=4)=0.1,P(ξ=5)=0.1
∴“购买该品牌汽车的3位顾客中至多有1位采用3期付款”的概率为P(A)=0.83+
•0.2•0.82=0.896;
(Ⅲ)η的可能取值为为1,1.5,2(单位:万元)
P(η=1)=P(ξ=1)=0.4,P(η=1.5)=P(ξ=2)+P(ξ=3)=0.4
P(η=2)=P(ξ=4)+P(ξ=5)=0.2
∴η的分布列为
∴Eη=1×0.4+1.5×0.4+2×0.2=1.2(万元)
| a |
| 100 |
(Ⅱ)记分期付款的期数为ξ,依题意得
P(ξ=1)=0.4,P(ξ=2)=0.2,P(ξ=3)=0.2,P(ξ=4)=0.1,P(ξ=5)=0.1
∴“购买该品牌汽车的3位顾客中至多有1位采用3期付款”的概率为P(A)=0.83+
| C | 1 3 |
(Ⅲ)η的可能取值为为1,1.5,2(单位:万元)
P(η=1)=P(ξ=1)=0.4,P(η=1.5)=P(ξ=2)+P(ξ=3)=0.4
P(η=2)=P(ξ=4)+P(ξ=5)=0.2
∴η的分布列为
| η | 1 | 1.5 | 2 |
| P | 0.4 | 0.4 | 0.2 |
点评:本题主要考查了离散型随机变量及其分布列,以及离散型随机变量的期望,同时考查了运算求解的能力,属于中档题.

练习册系列答案
相关题目
某品牌的汽车4S店,对最近100位采用分期付款的购车者进行统计,统计结果如右表所示:已知分3期付款的频率为0.2,4S店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元;分2期或3期付款其利润为1.5万元;分4期或5期付款,其利润为2万元.用η表示经销一辆汽车的利润.
(1)求表中的a,b值;
(2)若以频率作为概率,求事件A:“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的概率P(A);
(3)求η的分布列及数学期望Eη.
| 付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
| 频数 | 40 | 20 | a | 10 | b |
(2)若以频率作为概率,求事件A:“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的概率P(A);
(3)求η的分布列及数学期望Eη.
(本小题满分12分)某品牌的汽车4S店,对最近100位采用分期付款的购车者进行统计,统计结果如下表所示:已知分3期付款的频率为0.2,4S店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元,分2期或3期付款其利润为1.5万元;分4期或5期付款,其利润为2万元,用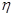 表示经销一辆汽车的利润。
表示经销一辆汽车的利润。
|
付款方工 |
分1期 |
分2期 |
分3期 |
分4期 |
分5期 |
|
频数 |
40 |
20 |
|
10 |
|
(1)求上表中的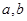 值;(2)若以频率作为概率,求事件A:“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的频率P(A);(3)求
值;(2)若以频率作为概率,求事件A:“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的频率P(A);(3)求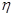 的分布列及数学期望E
的分布列及数学期望E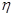 。
。
(本题满分12分)某品牌的汽车4S店,对最近100位采用分期付款的购车者进行统计,统计结果如右表所示:
|
付款方式 |
分l期 |
分2期 |
分3期 |
分4期 |
分5期 |
|
频数 |
40 |
20 |
a |
10 |
b |
已知分3期付款的频率为0.2 ,4S店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元;分2期或3期付款其利润为1.5万元;分4期或5期付款,其利润为2万元.用 表示经销一辆汽车的利润
表示经销一辆汽车的利润
(Ⅰ)求上表中a,b的值
(Ⅱ)若以频率作为概率,求事件A:“购买该品牌汽车的3位顾客中,至多有l位采用3期付款”的概率P(A)
(Ⅲ)求 的分布列及数学期望
的分布列及数学期望