题目内容
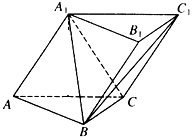
【题目】如图,在正方形ABCD中,点E,F分别是AB,BC的中点.将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于P. 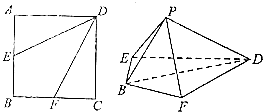
(1)求证:平面PBD⊥平面BFDE;
(2)求二面角P﹣DE﹣F的余弦值.
【答案】
(1)证明:由正方形ABCD知,∠DCF=∠DAE=90°,EF∥AC,BD⊥AC,EF⊥BD,
∵点E,F分别是AB,BC的中点.将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于P.
∴PD⊥PF,PD⊥PE,
∵PE∩PF=P,PE、PF平面PEF.
∴PD⊥平面PEF.
又∵EF平面PEF,
∴PD⊥EF,又BD∩PD=D,
∴EF⊥平面PBD,
又EF平面BFDE,∴平面PBD⊥平面BFDE
(2)解:连结BD、EF,交于点O,以O为原点,OF为x轴,OD为y轴,OP为z轴,建立空间直角坐标系,
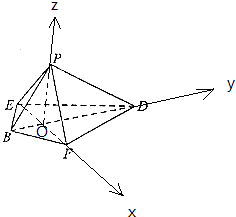
设在正方形ABCD的边长为2,则DO= ![]() ,
, ![]() =
= ![]() ,PE=PF=1,PO=
,PE=PF=1,PO= ![]() =
= ![]() ,
,
∴P(0,0, ![]() ),D(0,
),D(0, ![]() ,0),E(﹣
,0),E(﹣ ![]() ,0,0),F(
,0,0),F( ![]() ,0,0),
,0,0),
![]() =(﹣
=(﹣ ![]() ,﹣
,﹣ ![]() ,0),
,0), ![]() =(0,﹣
=(0,﹣ ![]() ,
, ![]() ),
), ![]() =(
=( ![]() ,﹣
,﹣ ![]() ,0),
,0),
设平面PDE的法向量 ![]() =(x,y,z),
=(x,y,z),
则 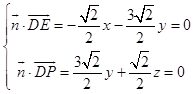 ,取y=1,则
,取y=1,则 ![]() =(﹣3,
=(﹣3, ![]() ,3),
,3),
平面DEF的法向量 ![]() =(0,0,1),
=(0,0,1),
设二面角P﹣DE﹣F的平面角为θ,
则cosθ= ![]() =
= ![]() =
= ![]() .
.
∴二面角P﹣DE﹣F的余弦值为 ![]() .
.
【解析】(1)推导出PD⊥PF,PD⊥PE,则PD⊥平面PEF,由此能证明平面PBD⊥平面BFDE.(2)连结BD、EF,交于点O,以O为原点,OF为x轴,OD为y轴,OP为z轴,建立空间直角坐标系,由此能求出二面角P﹣DE﹣F的余弦值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目