题目内容
已知y=f(x)是顶点在原点的二次函数,且方程f(x)=3-x有一个根x=2,则不等式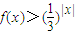 的解集是( )
的解集是( )A.(-∞,-2)∪(2,+∞)
B.(-2,2)
C.(0,2)
D.∅
【答案】分析:根据y=f(x)是顶点在原点的二次函数得到f(x)是偶函数,而y=3-|x|也是偶函数,根据f(x)=3-x有一个根x=2,即可求出所求.
解答:解:∵y=f(x)是顶点在原点的二次函数
∴设f(x)=ax2,是偶函数
∵方程f(x)=3-x有一个根x=2,
∴方程f(x)=3-|x| 有两个根x=±2
∴不等式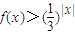 =3-|x|的解集为(-∞,-2)∪(2,+∞)
=3-|x|的解集为(-∞,-2)∪(2,+∞)
故选A
点评:本题主要考查了函数与方程的综合运用,以及不等式的解法,属于基础题.
解答:解:∵y=f(x)是顶点在原点的二次函数
∴设f(x)=ax2,是偶函数
∵方程f(x)=3-x有一个根x=2,
∴方程f(x)=3-|x| 有两个根x=±2
∴不等式
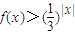 =3-|x|的解集为(-∞,-2)∪(2,+∞)
=3-|x|的解集为(-∞,-2)∪(2,+∞)故选A
点评:本题主要考查了函数与方程的综合运用,以及不等式的解法,属于基础题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 是“平顶型”函数,求出m,n的值.
是“平顶型”函数,求出m,n的值.