题目内容
（理）过圆锥曲线焦点F的直线被曲线截得的弦称为焦点弦，若抛物线y2=2px（p＞0）的焦点将焦点弦分成长为m，n的两段，则有结论
+
=
．借助获得这一结论的思想方法可以得到：若椭圆
+
=1 (a＞b＞0)的一个焦点将焦点弦分成长为m，n的两段，则
+
=
．
| 1 |
| m |
| 1 |
| n |
| 2 |
| p |
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| m |
| 1 |
| n |
| 2a |
| b2 |
| 2a |
| b2 |
分析：由类比推理，来得到关于椭圆的类似结论，易知在椭圆中有“
+
=
”求解即可．
| 1 |
| m |
| 1 |
| n |
| 2a |
| b2 |
解答：解：根据已知的结论，由类比推理得：
已知椭圆
+
=1（a＞b＞0），一个焦点将焦点弦分成长为m，n的两段，则
+
=
．
已知椭圆
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| m |
| 1 |
| n |
| 2a |
| b2 |
点评：本题主要考查类比推理，可以先猜测在抛物线中成立的命题在椭圆里面也成立．关于椭圆的一个恒等式“
+
=
”，是一个经常用到的式子，在以后的学习过程中希望大家多总结．
| 1 |
| m |
| 1 |
| n |
| 2a |
| b2 |
练习册系列答案
相关题目
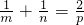．借助获得这一结论的思想方法可以得到：若椭圆
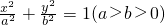的一个焦点将焦点弦分成长为m，n的两段，则
=________．