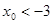题目内容
(12分)已知抛物线 的弦AB与直线y=1有公共点,且弦AB的中点N到y轴的距离为1,求弦AB长度的最大值,并求此直线AB所在的直线的方程.
的弦AB与直线y=1有公共点,且弦AB的中点N到y轴的距离为1,求弦AB长度的最大值,并求此直线AB所在的直线的方程.
【答案】
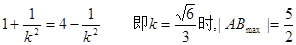
【解析】主要考查直线与抛物线的位置关系、弦长公式,考查分析问题解决问题的能力以及计算能力。
解:设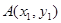 、
、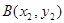 ,中点
,中点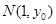
当AB直线的倾斜角90°时,AB直线方程是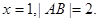 (2分)
(2分)
当AB直线的倾斜角不为90°时,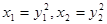 相减得
相减得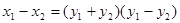
所以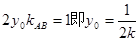 (4分)
(4分)
设AB直线方程为: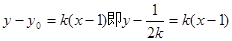 ,由于弦AB与直线y=1有公共点,故当y=1时,
,由于弦AB与直线y=1有公共点,故当y=1时,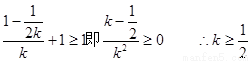
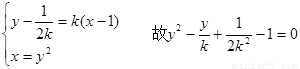
所以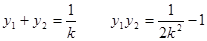 ,
,
故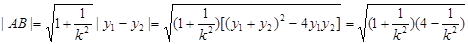
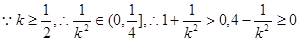
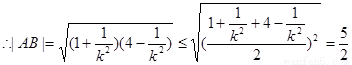
故当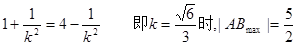 。
。
思路拓展:建立关于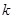 的函数关系式,是解答此题的关键。巧妙利用“弦长公式”及均值定理,达到解题目的。
的函数关系式,是解答此题的关键。巧妙利用“弦长公式”及均值定理,达到解题目的。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
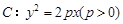 的焦点为F,准线为l,过F的直线与该抛物线交于A、B两点,设
的焦点为F,准线为l,过F的直线与该抛物线交于A、B两点,设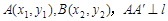 于
于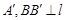 于
于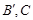 为弦AB的中点,则下列结论:①以AB为直径的圆必与准线l相切; ②
为弦AB的中点,则下列结论:①以AB为直径的圆必与准线l相切; ②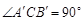 ;
; 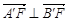 ; ④
; ④ ; ⑤.
; ⑤.
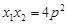
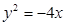 的焦点为F,其准线与x轴交于点
的焦点为F,其准线与x轴交于点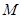 ,过点
,过点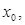 0)。
0)。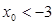 ;
;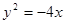 的焦点为F,其准线与x轴交于点M,过点M作斜率为k的直线l交抛物线于A、B两点,.
的焦点为F,其准线与x轴交于点M,过点M作斜率为k的直线l交抛物线于A、B两点,. O),求证:
O),求证:
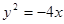 的焦点为F,其准线与x轴交于点M,过点M作斜率为k的直线l交抛物线于A、B两点,.
的焦点为F,其准线与x轴交于点M,过点M作斜率为k的直线l交抛物线于A、B两点,.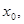 O),求证:
O),求证: