题目内容
设函数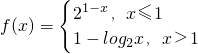 ,则不等式f(x)≤2的解集为________.
,则不等式f(x)≤2的解集为________.
[0,+∞)
分析:根据题意,分情况讨论:x≤1时,f(x)=21-x≤2;x>1时,f(x)=1-log2x≤2,分别求解即可.
解答:x≤1时,f(x)=21-x≤2,
解得 x≥0,因为x≤1,故0≤x≤1;
x>1时,f(x)=1-log2x≤2,解得x≥ ,故x>1.
,故x>1.
综上所述,不等式f(x)≤2的解集为[0,+∞).
故答案为:[0,+∞).
点评:本题考查分段函数、解不等式问题、对数函数的单调性与特殊点,属基本题,难度不大.
分析:根据题意,分情况讨论:x≤1时,f(x)=21-x≤2;x>1时,f(x)=1-log2x≤2,分别求解即可.
解答:x≤1时,f(x)=21-x≤2,
解得 x≥0,因为x≤1,故0≤x≤1;
x>1时,f(x)=1-log2x≤2,解得x≥
 ,故x>1.
,故x>1.综上所述,不等式f(x)≤2的解集为[0,+∞).
故答案为:[0,+∞).
点评:本题考查分段函数、解不等式问题、对数函数的单调性与特殊点,属基本题,难度不大.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
 ,则不等式f(x)≤2的解集为 .
,则不等式f(x)≤2的解集为 . ,则不等式f(x)≤2的解集为 .
,则不等式f(x)≤2的解集为 . ,则不等式f(x)≤2的解集为 .
,则不等式f(x)≤2的解集为 . ,则不等式f(x)≤2的解集为 .
,则不等式f(x)≤2的解集为 . ,则不等式f(x)≤2的解集为 .
,则不等式f(x)≤2的解集为 .