题目内容
（本题满分12分）已知如图，在四棱锥P—ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，过D与PB垂直的平面分别交PB、PC于F、E.
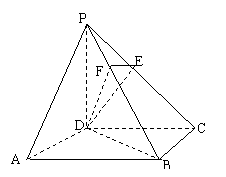（1）求证：DE⊥PC；
（2）当PA//平面EDB时，求二面角E—BD—C的正切值.
（本题满分12分）（1）证明：
平面DEF
平面ABCD 又
………4分
从而DE⊥平面PBC
………………6分
（2）解：连AC交BD于O，连EO,由PA//平面EDB
及平面EDB∩平面PAC于EO
知PA//EO ………………7分
是正方形ABCD的对角线AC的中点 
为PC的中点
又
……………………………8分
设PD=DC=a，取DC的中点H，作HG//CO交BD于G，
则HG⊥DB，EH//PD 
平面CDB。
由三垂线定理知EG⊥BD
故
为二面角E—BD—C的一个平面角。 ………………10分
易求得
∴二面角E—BD—C的正切值为
(用向量法做参考给分) …………12分
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
的三个内角
、
、
所对的边分别为
、
、
.
，且
.（1）求
.求
.
，
的等比中项。
是等差数列；（2）若
的前n项和为Tn,求Tn。
：
的长轴长是短轴长的
倍，
，
是它的左，右焦点．
，且
，
，求
作以
（
是切点），且使
，求动点
的长轴，短轴端点分别是A,B，从椭圆上一点M向x轴作垂线，恰好通过椭圆的左焦点，向量
与
是共线向量
分别是左右焦点，求
的取值范围