题目内容
已知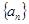 是公比为
是公比为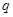 的等比数列,且
的等比数列,且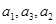 成等差数列.
成等差数列.
⑴求q的值;
⑵设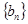 是以2为首项,
是以2为首项,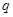 为公差的等差数列,其前
为公差的等差数列,其前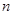 项和为
项和为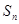 ,当n≥2时,比较
,当n≥2时,比较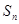 与
与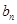 的大小,并说明理由.
的大小,并说明理由.
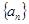 是公比为
是公比为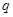 的等比数列,且
的等比数列,且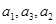 成等差数列.
成等差数列.⑴求q的值;
⑵设
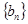 是以2为首项,
是以2为首项,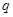 为公差的等差数列,其前
为公差的等差数列,其前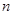 项和为
项和为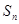 ,当n≥2时,比较
,当n≥2时,比较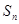 与
与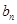 的大小,并说明理由.
的大小,并说明理由.(1)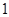 或
或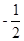 (2)详见解析.
(2)详见解析.
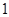 或
或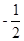 (2)详见解析.
(2)详见解析.试题分析:(1)等比数列中的等差数列问题,解题关键要根据题意列方程,该题可利用等差中项列方程,可得
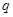 的值;(2)求出等差数列
的值;(2)求出等差数列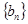 的前n项和
的前n项和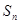 和通项公式
和通项公式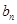 ,可以根据解析式的特点选择作商比较或者作差比较法,
,可以根据解析式的特点选择作商比较或者作差比较法,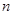 的范围要注意.
的范围要注意.试题解析:(1)由题设
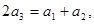 即
即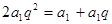
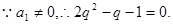
∴
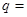
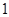 或
或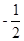 .
.(2)若
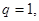 则
则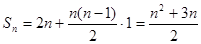 ,
,当
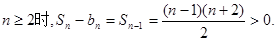 故
故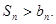
若
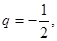 则
则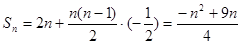 ,
,当

故对于
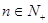 ,当
,当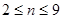 时,
时,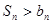 ;当
;当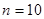 时,
时,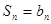 ;当
;当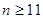 时,
时,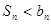 .
. 和;2、比较法;3、等比数列的通项公式.
和;2、比较法;3、等比数列的通项公式.
练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
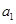 、
、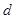 为实数,首项为
为实数,首项为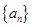 的前
的前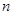 项和为
项和为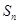 ,满足
,满足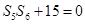 ,
,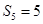 .
.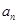 及
及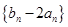 是首项为
是首项为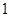 ,公比为
,公比为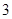 的等比数列,求数列
的等比数列,求数列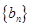 的通项公式及其前
的通项公式及其前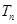 .
.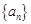 满足:
满足: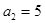 ,
,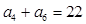 .
.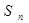 .
.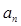 及
及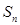 ;
;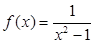 ,
,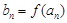 (
(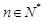 ),求数列
),求数列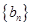 的前
的前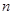 项和
项和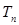 .
.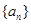 中,若
中,若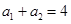 ,
, 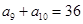 ,则
,则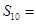 .
. 中,
中, ,
, ,且
,且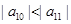 ,
,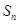 为其前
为其前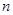 项之和,则( )
项之和,则( ) 都小于零,
都小于零, 都大于零
都大于零 都小于零,
都小于零, 都大于零
都大于零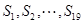 都小于零,
都小于零,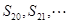 都大于零
都大于零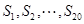 都小于零,
都小于零,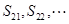 都大于零
都大于零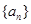 的前
的前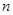 项和为
项和为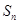 .若
.若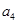 是
是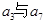 的等比中项,
的等比中项, 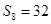 ,则
,则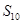 =( ).
=( ). 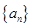 满足
满足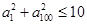 ,则
,则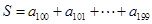 的最大值为( )
的最大值为( )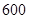

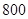
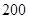
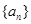 的前
的前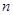 项和为
项和为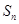 ,若
,若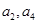 是方程
是方程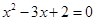 的两个实数根,则
的两个实数根,则 .
.