题目内容

已知△ABC三边长分别为1、2、a（其中a∈R+），“△ABC为锐角三角形”的充要条件是：“a∈
 
”．
分析：由已知中△ABC三边长分别为1、2、a，我们易根据余弦定理的推论得到△ABC为锐角三角形的充要条件，但要注意由于a的大小不确定，故2与a边均有可能为最大边，故要分类讨论．
解答：解：∵△ABC三边长分别为1、2、a
又∵△ABC为锐角三角形
当2为最大边时，a＞
22-12
=
3

当a为最大边时，a＜
22+12
=
5

∴a∈(
3
，
5
)
故答案为：(
3
，
5
)
点评：本题考查的知识点是充要条件，三角形的形状判断，其中解答本题的关键是余弦定理的推论--三角形形状的判定方法：a，b，c为△ABC 的三边，其中c为最大边，则a2+b2＞c2?△ABC 为锐角三角形的充要条件．
练习册系列答案
相关题目
已知△ABC的内角A、B、C所对的边分别为a，b，c，且△ABC的外接圆半径为R，
AB
•
AC
=9．sinB=cosAsinC．
（1）求△ABC的三边的长；
（2）设P是△ABC（含边界）内的一点，P到三边AC、BC、AB的距离分别是x、y、z．
①写出x、y、z．所满足的等量关系；
②利用线性规划相关知识求出x+y+z的取值范围．
记实数x1，x2…xn中的最大数为max{x1，x2…xn}，最小数为min{x1，x2…xn}．已知△ABC的三边边长为a，b，c（a≤b≤c），定义它的倾斜度为t=max{
a
b
，
b
c
，
c
a
}•min{
a
b
，
b
c
，
c
a
}，则“t=1”是“△ABC为等边三角形”的
 
．（填充分不必要条件、必要不充分条件、充要条件、既不充分也不必要条件）．
已知△ABC的三边长分别是2m+3,m2+2m,m2+3m+3(m＞0)，则最大内角的度数是(    )

A.150°                B.135°                 C.120°                D.90°

（本小题满分10分）

已知△ABC的三边长都是有理数。

求证cosA是有理数；（2）求证：对任意正整数n，cosnA是有理数。

(本小题满分12分)
已知△ABC的三边长为a、b、c，且其中任意两边长均不相等.若  成等差数列.
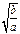(1)比较 与的大小，并证明你的结论;
(2)求证B不可能是钝角.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网