题目内容
当对数函数y=logax(a>0且a≠1)的图象至少经过区域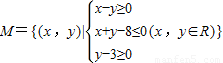 内的一个点时,实数a的取值范围为 .
内的一个点时,实数a的取值范围为 .
【答案】分析:先依据集合M中的不等式组,结合二元一次不等式(组)与平面区域的关系画出其表示的平面区域,再利用函数f(x)=logax的图象特征,结合区域的角上的点即可解决问题.
解答: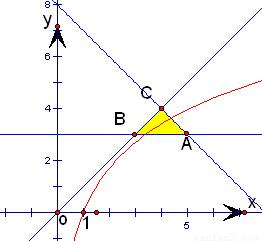 解:作出区域D的图象,图中阴影部分.
解:作出区域D的图象,图中阴影部分.
联系函数f(x)=logax的图象,能够看出,只有当a>1时才有可能经过区域,
当图象经过区域的边界点A(5,3)时,a可以取到最大值: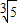 ,
,
当图象经过区域的边界点C(4,4)时,a可以取到最小值: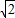 ,
,
函数f(x)=logax(a>1)的图象必然经过区域内的点.
则a的取值范围是[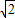 ,
,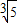 ].
].
故答案为:[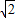 ,
,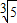 ].
].
点评:这是一道灵活的线性规划问题,本题主要考查了用平面区域二元一次不等式组、指数函数的图象与性质,本题的注意点是要用运动的观点看待问题,应用简单的转化思想和数形结合的思想解决问题.
解答:
 解:作出区域D的图象,图中阴影部分.
解:作出区域D的图象,图中阴影部分.联系函数f(x)=logax的图象,能够看出,只有当a>1时才有可能经过区域,
当图象经过区域的边界点A(5,3)时,a可以取到最大值:
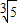 ,
,当图象经过区域的边界点C(4,4)时,a可以取到最小值:
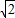 ,
,函数f(x)=logax(a>1)的图象必然经过区域内的点.
则a的取值范围是[
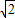 ,
,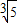 ].
].故答案为:[
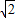 ,
,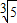 ].
].点评:这是一道灵活的线性规划问题,本题主要考查了用平面区域二元一次不等式组、指数函数的图象与性质,本题的注意点是要用运动的观点看待问题,应用简单的转化思想和数形结合的思想解决问题.

练习册系列答案
相关题目
当对数函数y=logax(a>0且a≠1)的图象至少经过区域
内的一个点时,实数a的取值范围为( )
|
A、[
| ||||||
B、[
| ||||||
C、[
| ||||||
D、[
|
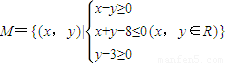 内的一个点时,实数a的取值范围为 .
内的一个点时,实数a的取值范围为 . 内的一个点时,实数a的取值范围为( )。
内的一个点时,实数a的取值范围为( )。