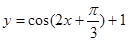题目内容
设 是正实数,函数
是正实数,函数 在
在 上是增函数,那么
上是增函数,那么 的最大值是
的最大值是
A. | B.2 | C. | D.3 |
A
解析试题分析:因为x∈ ,∴
,∴ ,
,
又函数f(x)=2sinx的增区间为[ ]
]
∴ 且
且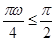 解得:0≤ω≤
解得:0≤ω≤
∴ 的最大值为
的最大值为 ,选A。
,选A。
考点:本题主要考查正弦函数的性质,简单不等式组的解法。
点评:简单题,作为选择题,我们可以利用将选项代入检验的方法。这里从y=sinx的单调区间入手考虑求解。

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
已知 和
和 都是锐角,且
都是锐角,且 ,
, ,则
,则 的值是( )
的值是( )
A. | B. | C. | D. |
为了得到函数 的图像,需要把函数
的图像,需要把函数 图像上的所有点
图像上的所有点
A.横坐标缩短到原来的 倍,再向右平移 倍,再向右平移 个单位长度 个单位长度 |
B.横坐标伸长到原来的 倍,再向右平移 倍,再向右平移 个单位长度 个单位长度 |
C.横坐标缩短到原来的 倍,再向左平移 倍,再向左平移 个单位长度 个单位长度 |
D.横坐标伸长到原来的 倍,再向左平移 倍,再向左平移 个单位长度 个单位长度 |
若函数 对称,那么
对称,那么 =( )
=( )
A. | B.- | C.1 | D.-1 |
已知函数
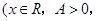
 )的图象(部分)如图所示,则
)的图象(部分)如图所示,则 的解析式是 ( )
的解析式是 ( )
A. |
B. |
C. |
D. |
把函数 的图象向左平移
的图象向左平移 后,所得函数的解析式是
后,所得函数的解析式是
A. | B. | C. | D. |
已知 =
= ,
, ,则
,则 为( )
为( )
A. | B. | C. | D. |
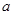 是实数,则函数
是实数,则函数 的图象不可能是( )
的图象不可能是( )
 图象上的所有点向左平移
图象上的所有点向左平移 个单位长度,再把所得图像向上平移1个单位长度,所得图象的函数解析式是( )
个单位长度,再把所得图像向上平移1个单位长度,所得图象的函数解析式是( )