题目内容
已知函数f(x)=2x+1定义在R上,
(1)若f(x)可以表示为一个偶函数g(x)与一个奇函数h(x)之和,设h(x)=t,p(t)=g(2x)+2mh(x)+m2-m-1(m∈R),求出p(t)的解析式;
(2)若p(t)≥m2-m-1对于x∈[1,2]恒成立,求m的取值范围;
(3)若方程p(p(t))=0无实根,求m的取值范围。
(1)若f(x)可以表示为一个偶函数g(x)与一个奇函数h(x)之和,设h(x)=t,p(t)=g(2x)+2mh(x)+m2-m-1(m∈R),求出p(t)的解析式;
(2)若p(t)≥m2-m-1对于x∈[1,2]恒成立,求m的取值范围;
(3)若方程p(p(t))=0无实根,求m的取值范围。
解:(1)假设f(x)=g(x)+h(x)①,其中g(x)为偶函数,h(x)为奇函数,
则有f(-x)=g(-x)+h(-x),即f(-x)=g(x)-h(x),②
由①②解得g(x)=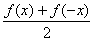 ,h(x)=
,h(x)=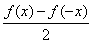 ,
,
∵f(x)定义在R上,
∴g(x),h(x)都定义在R上,
∵g(-x)=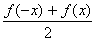 =g(x),h(-x)=
=g(x),h(-x)=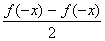 =-h(x),
=-h(x),
∴g(x)是偶函数,h(x)是奇函数,
∵f(x)=2x+1,
∴g(x)=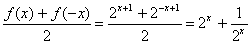 ,
,
h(x)=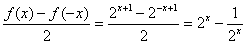 ,
,
由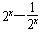 =t,则t∈R,
=t,则t∈R,
平方得t2= ,
,
∴g(2x)=22x+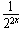 =t2+2,
=t2+2,
∴p(t)=t2+2mt+m2-m+1。
(2)∵t=h(x)对于x∈[1,2]单调递增,
∴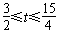 ,
,
p(t)=t2+2mt+m2-m+1≥m2-m-1对于t∈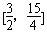 恒成立,
恒成立,
∴m≥-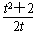 对于t∈
对于t∈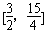 恒成立,
恒成立,
令φ(t)=-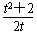 ,则φ′(t)=
,则φ′(t)=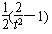 ,
,
∵t∈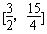 ,∴φ′(t)=
,∴φ′(t)=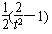 <0,
<0,
故φ(t)=-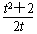 在t∈
在t∈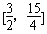 上单调递减,
上单调递减,
∴φ(t)max=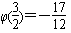 ,
,
∴m≥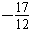 为m的取值范围.
为m的取值范围.
(3)由(1)得p(p(t))=[p(t)]2+2mp(t)+m2-m+1,
若p(p(t))=0无实根,即[p(t)]2+2mp(t)+m2-m+1=0①无实根,
方程①的判别式△=4m2-4(m2-m+1)=4(m-1),
1°当方程①的判别式△<0,即m<1时,方程①无实根;
2°当方程①的判别式△≥0,
即m≥1时,方程①有两个实根p(t)=t2+2mt+m2-m+1=-m±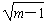 ,
,
即t2+2mt+m2+1±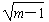 =0②,
=0②,
只要方程②无实根,故其判别式△=4m2-4(m2+1±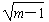 )<0,
)<0,
即得-1-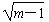 <0③,且-1+
<0③,且-1+ <0④,
<0④,
∵m≥1,③恒成立,
由④解得m<2,
∴③④同时成立得1≤m<2;
综上,m的取值范围为m<2。
则有f(-x)=g(-x)+h(-x),即f(-x)=g(x)-h(x),②
由①②解得g(x)=
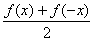 ,h(x)=
,h(x)=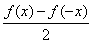 ,
,∵f(x)定义在R上,
∴g(x),h(x)都定义在R上,
∵g(-x)=
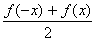 =g(x),h(-x)=
=g(x),h(-x)=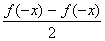 =-h(x),
=-h(x),∴g(x)是偶函数,h(x)是奇函数,
∵f(x)=2x+1,
∴g(x)=
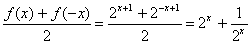 ,
,h(x)=
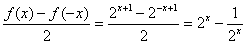 ,
,由
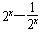 =t,则t∈R,
=t,则t∈R,平方得t2=
 ,
,∴g(2x)=22x+
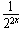 =t2+2,
=t2+2,∴p(t)=t2+2mt+m2-m+1。
(2)∵t=h(x)对于x∈[1,2]单调递增,
∴
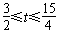 ,
,p(t)=t2+2mt+m2-m+1≥m2-m-1对于t∈
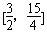 恒成立,
恒成立, ∴m≥-
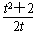 对于t∈
对于t∈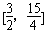 恒成立,
恒成立,令φ(t)=-
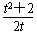 ,则φ′(t)=
,则φ′(t)=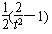 ,
,∵t∈
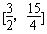 ,∴φ′(t)=
,∴φ′(t)=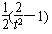 <0,
<0,故φ(t)=-
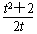 在t∈
在t∈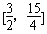 上单调递减,
上单调递减,∴φ(t)max=
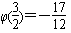 ,
,∴m≥
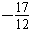 为m的取值范围.
为m的取值范围.(3)由(1)得p(p(t))=[p(t)]2+2mp(t)+m2-m+1,
若p(p(t))=0无实根,即[p(t)]2+2mp(t)+m2-m+1=0①无实根,
方程①的判别式△=4m2-4(m2-m+1)=4(m-1),
1°当方程①的判别式△<0,即m<1时,方程①无实根;
2°当方程①的判别式△≥0,
即m≥1时,方程①有两个实根p(t)=t2+2mt+m2-m+1=-m±
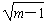 ,
,即t2+2mt+m2+1±
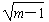 =0②,
=0②,只要方程②无实根,故其判别式△=4m2-4(m2+1±
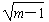 )<0,
)<0,即得-1-
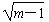 <0③,且-1+
<0③,且-1+ <0④,
<0④, ∵m≥1,③恒成立,
由④解得m<2,
∴③④同时成立得1≤m<2;
综上,m的取值范围为m<2。

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目