题目内容
已知F是抛物线y2=x的焦点，A，B是该抛物线上的两点，
，则线
段AB的中点到y轴的距离为
A． | B．1 | C． | D． |
C
解析考点：抛物线的定义．
分析：根据抛物线的方程求出准线方程，利用抛物线的定义抛物线上的点到焦点的距离等于到准线的距离，列出方程求出A，B的中点横坐标，求出线段AB的中点到y轴的距离．
解答：解：∵F是抛物线y2=x他焦点
F（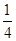
，n）准线方程x=-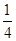
设A（x1，y1），B（x2，y2）
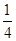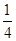∴|AF|+|BF|=x1++x2+=3
解得x1+x2=
∴线段AB他3点横坐标为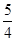
∴线段AB他3点到y轴他距离为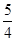
故答案为：C．
点评：本题主要考查抛物线的定义、标准方程，以及简单性质的应用，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
已知F是抛物线y2=x的焦点，A，B是该抛物线上的两点，|AF|+|BF|=3，则线段AB的中点到y轴的距离为（ ）
A、
| ||
| B、1 | ||
C、
| ||
D、
|
（2010•重庆一模）已知F是抛物线y2=4x的焦点，Q是抛物线的准线与x轴的交点，直线l经过点Q．