题目内容
定义在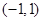 上的函数
上的函数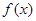 满足:对任意
满足:对任意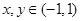 ,
,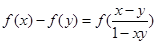 恒成立.有下列结论:①
恒成立.有下列结论:①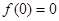 ;②函数
;②函数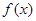 为
为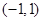 上的奇函数;③函数
上的奇函数;③函数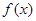 是定义域内的增函数;④若
是定义域内的增函数;④若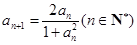 ,且
,且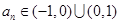 ,则数列
,则数列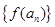 为等比数列.
为等比数列.
其中你认为正确的所有结论的序号是 .
【答案】
①②④
【解析】
试题分析:因为已知中,函数满足对任意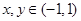 ,
,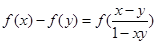 恒成立
恒成立
那么可知f(0)-f(0)=f(0),故有f(0)=0,故命题1正确。
命题2中,令0=x,y=x则f(0)-f(x)=f(-x),f(-x)+f(x)=0,可知为奇函数。
故正确。
命题3中,令x=1,y=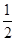 .那么可知得到f(
.那么可知得到f(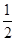 )=0,显然不符合单调函数定义,错误。
)=0,显然不符合单调函数定义,错误。
命题4总,由于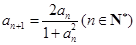 ,且
,且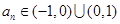 ,则数列
,则数列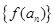 为等比数列,故成立。正确的序号为①②④
为等比数列,故成立。正确的序号为①②④
考点:本试题主要是考查了函数的单调性和数列的综合运用。
点评:解决该试题的关键是利用抽象函数的表达式,进行合理的赋值,然后结合函数的奇偶性的性质很单调性的性质来求解分析得到结论。体现了抽象函数的赋值思想的运用,属于中档题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
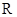 上的函数
上的函数 满足
满足 ,且
,且 在
在 ,则不等式
,则不等式 的解集为( )
的解集为( )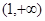 B.
B.
 C.
C.
 D.
D.
 上的函数
上的函数 满足
满足 ,
, ,则不等式
,则不等式 的解集为_ .
的解集为_ .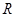 上的函数
上的函数 满足
满足 ,则
,则

 上的函数
上的函数 满足
满足 且
且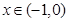 时,
时, 则
则 ( )
( ) (B)
(B) (C)
(C) (D)
(D)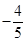
 上的函数
上的函数 满足:对于
满足:对于 ,总有
,总有 ,则下列说法正确的是:( )
,则下列说法正确的是:( ) 是奇函数 (B)
是奇函数 (B) 是奇函数(C)
是奇函数(C) 是奇函数(D)
是奇函数(D) 是奇函数
是奇函数