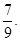题目内容
一个袋中有10个大小相同的黑球、白球和红球,已知从袋中任意摸出一个球,得到黑球的概率是| 2 |
| 5 |
| 7 |
| 9 |
(1)求袋中白球的个数;
(2)若将其中的红球拿出,从剩余的球中一次摸出3个球,求恰好摸到2个白球的概率;
(3)在(2)的条件下,一次摸出3个球,求取得白球数X的数学期望.
分析:(1)设袋中白球数为n,根据“从中任摸2个球至少得到1个白球”与“任取两球无白球”为对立事件可得答案.
(2)由题意可得:袋中的黑球有4个,所以红球一个.所以袋中有4黑5白9个球,根据古典概率模型的公式可得答案.
(3)由题意可得:X服从参数为N=9,M=5,n=3的超几何分布,进而根据有关公式可得答案.
(2)由题意可得:袋中的黑球有4个,所以红球一个.所以袋中有4黑5白9个球,根据古典概率模型的公式可得答案.
(3)由题意可得:X服从参数为N=9,M=5,n=3的超几何分布,进而根据有关公式可得答案.
解答:解:(1)设袋中白球数为n.
设从中任摸2个球至少得到1个白球为事件A,任取两球无白球为事件
,
所以P(
)=1-
=
,
解得n=5,即袋中有5个白球.----------------------(4分)
(2)由题意可得:袋中的黑球有10×
=4个,所以红球一个.
若拿掉红球,则袋中有4黑5白9个球.
所以恰好摸到2个白球的概率=
=
------------------------(8分)
(3)设X表示摸出白球的个数,则X服从参数为N=9,M=5,n=3的超几何分布,
所以E(X)=
=
=
------------------(12分)
设从中任摸2个球至少得到1个白球为事件A,任取两球无白球为事件
. |
| A |
所以P(
. |
| A |
| ||
|
| 2 |
| 9 |
解得n=5,即袋中有5个白球.----------------------(4分)
(2)由题意可得:袋中的黑球有10×
| 2 |
| 5 |
若拿掉红球,则袋中有4黑5白9个球.
所以恰好摸到2个白球的概率=
| ||||
|
| 10 |
| 21 |
(3)设X表示摸出白球的个数,则X服从参数为N=9,M=5,n=3的超几何分布,
所以E(X)=
| nM |
| N |
| 3×5 |
| 9 |
| 5 |
| 3 |
点评:本题主要考查排列组合、概率等基础知识,同时考查逻辑思维能力和数学应用能力,考查对立事件的概率、古典概型问题以及超几何分布,是一个综合题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是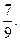
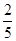 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是