题目内容
设函数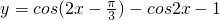
(1)求函数f(x)的最小正周期和单调递增区间;
(2)若函数y=f(x)-k在[0,π)内恰有两个零点,求实数k的取值范围.
解:(1)f(x)=cos2xcos +sin2xsin
+sin2xsin -cos2x-1
-cos2x-1
= sin2x-
sin2x- cos2x-1=sin(2x-
cos2x-1=sin(2x- )-1…3分
)-1…3分
∴函数f(x)的最小正周期是T= =π,…5分
=π,…5分
由2kπ- ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈Z解得kπ-
,k∈Z解得kπ- ≤x≤kπ+
≤x≤kπ+ ,
,
∴函数f(x)的单调递增区间是[kπ- ,kπ+
,kπ+ ](k∈Z)…7分
](k∈Z)…7分
(2)∵0≤x<π,f(x)的最小正周期是π,
∴-1≤sin(2x- )≤1,
)≤1,
∴-2≤f(x)≤0,…9分
又∵函数y=f(x)-k在(0,π)内恰有两个零点,
∴-2<k<0,
∴k的取值范围是(-2,0)…12分
分析:(1)将y=cos(2x- )-cos2x-1转化为y=sin(2x-
)-cos2x-1转化为y=sin(2x- )-1,即可求得函数f(x)的最小正周期和单调递增区间;
)-1,即可求得函数f(x)的最小正周期和单调递增区间;
(2)依题意可求得-1≤sin(2x- )≤1,从而有-2≤f(x)≤0,继而得-2<k<0.
)≤1,从而有-2≤f(x)≤0,继而得-2<k<0.
点评:本题考查三角函数中的恒等变换应用,考查函数的零点与方程根的关系,考查三角函数的周期性及其求法,考查复合函数的单调性,属于中档题.
 +sin2xsin
+sin2xsin -cos2x-1
-cos2x-1=
 sin2x-
sin2x- cos2x-1=sin(2x-
cos2x-1=sin(2x- )-1…3分
)-1…3分∴函数f(x)的最小正周期是T=
 =π,…5分
=π,…5分由2kπ-
 ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈Z解得kπ-
,k∈Z解得kπ- ≤x≤kπ+
≤x≤kπ+ ,
,∴函数f(x)的单调递增区间是[kπ-
 ,kπ+
,kπ+ ](k∈Z)…7分
](k∈Z)…7分(2)∵0≤x<π,f(x)的最小正周期是π,
∴-1≤sin(2x-
 )≤1,
)≤1,∴-2≤f(x)≤0,…9分
又∵函数y=f(x)-k在(0,π)内恰有两个零点,
∴-2<k<0,
∴k的取值范围是(-2,0)…12分
分析:(1)将y=cos(2x-
 )-cos2x-1转化为y=sin(2x-
)-cos2x-1转化为y=sin(2x- )-1,即可求得函数f(x)的最小正周期和单调递增区间;
)-1,即可求得函数f(x)的最小正周期和单调递增区间;(2)依题意可求得-1≤sin(2x-
 )≤1,从而有-2≤f(x)≤0,继而得-2<k<0.
)≤1,从而有-2≤f(x)≤0,继而得-2<k<0.点评:本题考查三角函数中的恒等变换应用,考查函数的零点与方程根的关系,考查三角函数的周期性及其求法,考查复合函数的单调性,属于中档题.

练习册系列答案
相关题目
 设函数
设函数 (2009•成都模拟)设函数
(2009•成都模拟)设函数
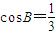 ,
,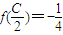 ,且C为锐角,求sinA的值.
,且C为锐角,求sinA的值.