题目内容
第十一届西博会于2010年10月22日至26日在蓉举行,本届西博会以“绿色改变生活,技术引领发展”为主题.如此重要的国际盛会,自然少不了志愿者这支重要力量,“志愿者,西博会最亮丽的风景线”,通过他们的努力和付出,已把志愿者服务精神的种子播撒到人们心中.某大学对参加了本次西博会的该校志愿者实施“社会教育实践”学分考核,因该批志愿者表现良好,该大学决定考核只有合格和优秀两个等次,若某志愿者考核为合格,授予0.5个学分;考核为优秀,授予1个学分.假设该校志愿者甲、乙、丙考核为优秀的概率分别为| 4 |
| 5 |
| 2 |
| 3 |
| 2 |
| 3 |
(1)求在这次考核中,志愿者甲、乙、两三人中至少有一名考核为优秀的概率;
(2)记这这次考核中甲、乙、丙三名志愿者所得学分之和为随机变量ξ,求随机变量ξ的分布列和数学期望Eξ.
分析:(I)由已知中,志愿者甲、乙、两三人中至少有一名考核为优秀,是“志愿者甲、乙、两三人中没有考核为优秀”,这个事件的对立事件,利用对立事件概率减法公式,即可求出答案.
(II)根据甲、乙、丙三名志愿者所得学分之和为随机变量ξ,则ξ的可能取值为
、2、
、3,分别计算出对应的概率,即可得到随机变量ξ的分布列,代入数学期望公式,即可得到数学期望Eξ.
(II)根据甲、乙、丙三名志愿者所得学分之和为随机变量ξ,则ξ的可能取值为
| 3 |
| 2 |
| 5 |
| 2 |
解答:解:(Ⅰ)记甲、乙、丙考核为优秀依次为事件A、B、C,
“志愿者甲、乙、两三人中至少有一名考核为优秀”为事件E,
事件A、B、C相互独立,
事件
•
•
与E是对立事件;
P(E)=1-P(
•
•
)=1-
×
×
=
;
(Ⅱ)根据题意,ξ的可能取值为
、2、
、3,
P(ξ=
)=P(
•
•
)=
,
P(ξ=2)=P(A•
•
)+P(
•B•
)+P(
•
•C)=
,
P(ξ=
)=P(A•B•
)+P(
•B•C)+P(A•
•C)=
,
P(ξ=3)=P(A•B•C)=
∴ξ的分布列为
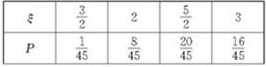
∴Eξ=
×
+2×
+
×
+3×
=
“志愿者甲、乙、两三人中至少有一名考核为优秀”为事件E,
事件A、B、C相互独立,
事件
. |
| A |
. |
| B |
. |
| C |
P(E)=1-P(
. |
| A |
. |
| B |
. |
| C |
| 1 |
| 5 |
| 1 |
| 3 |
| 1 |
| 3 |
| 44 |
| 45 |
(Ⅱ)根据题意,ξ的可能取值为
| 3 |
| 2 |
| 5 |
| 2 |
P(ξ=
| 3 |
| 2 |
. |
| A |
. |
| B |
. |
| C |
| 1 |
| 45 |
P(ξ=2)=P(A•
. |
| B |
. |
| C |
. |
| A |
. |
| C |
. |
| A |
. |
| B |
| 8 |
| 45 |
P(ξ=
| 5 |
| 2 |
. |
| C |
. |
| A |
. |
| B |
| 20 |
| 45 |
P(ξ=3)=P(A•B•C)=
| 16 |
| 45 |
∴ξ的分布列为

∴Eξ=
| 3 |
| 2 |
| 1 |
| 45 |
| 8 |
| 45 |
| 5 |
| 2 |
| 20 |
| 45 |
| 16 |
| 45 |
| 77 |
| 30 |
点评:本题考查的知识点是相互独立事件的概率乘法公式,离散型随机变量及其分布列,离散型随机变量的期望,在计算随机变量ξ的分布列时,一定要注意分类时要不重分,不漏分.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
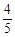 、
、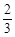 、
、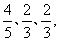 他们考核所得的等次相互独立。
他们考核所得的等次相互独立。 、
、 、
、 ,他们考核所得的等次相互独立.
,他们考核所得的等次相互独立.