题目内容
为了解某校学生参加某项测试的情况,从该校学生中随机抽取了6位同学,这6位同学的成绩(分数)如茎叶图所示.
⑴求这6位同学成绩的平均数和标准差;
⑵从这6位同学中随机选出两位同学来分析成绩的分布情况,求这两位同学中恰有一位同学成绩低于平均分的概率.
⑴这6位同学的成绩平均数为81;标准差为7;⑵ .
.
解析试题分析:⑴代入平均数及标准差的公式即得;⑵由(1)可得平均分为81,所以低于平均分的有4人.现从中抽取2人,首先将所有可能结果一一列举出来,然后数出其中恰有一个低于平均分的所有结果,二者相除即得所求概率
试题解析:⑴这6位同学的成绩平均数为 .
.
又 .
.
故这6位问学成绩的标准差为s=7 .6分
⑵从6位同学中随机选取2位同学,包含的基本事件空间为(76,76)、(76,78)、
(76,78)、(76,82)、(76,96)、(76,78)、(76,78)、(76,82)、(76,96)、(78,78)、
(78,82)、(78,96)、(78,82)、(78,96)、(82,96)15个基本事件。其中括号内数字分别表示2位同学的成绩.
记“选出的2位问学中,恰有1位同学的成绩低于平均分”为事件A,则事件A包含的基本事件为(76,82)、(76,96)、(76,82)、(76,96)、(78,82)、(78,96)、(78,82)、(78,96)共8个基本事件,则 。
。
故从6位同学中随机选取2位同学,恰有1位同学的成绩低于平均分的概率为 . ..12分
. ..12分
考点:1、平均数与标准差;2、古典概型.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 表示的平面区域为
表示的平面区域为 ,在区域
,在区域 ,则
,则 的概率为________.
的概率为________.
 ,2;
,2; ,3;
,3; ,4;
,4; ,5;
,5; ,4;
,4; ,2.则样本在
,2.则样本在 上的频率是 .
上的频率是 . ,
,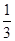 ,
, ,则此密码能被译出的概率为________.
,则此密码能被译出的概率为________. ,P(B)=
,P(B)= ,则P(A
,则P(A )=________;P(
)=________;P(