题目内容
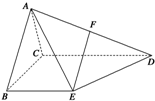 四棱锥A-BCDE的侧面ABC是等边三角形,EB⊥平面ABC,DC⊥平面ABC,BE=1,BC=CD=2,F是棱AD的中点.
四棱锥A-BCDE的侧面ABC是等边三角形,EB⊥平面ABC,DC⊥平面ABC,BE=1,BC=CD=2,F是棱AD的中点.(1)求证:EF∥平面ABC;
(2)求四棱锥A-BCDE的体积.
分析:(1)取AC中点M,连接FM、BM,可由中位线定理,线面垂直的性质定理,证得四边形BEFM是平行四边形,进而EF∥BM,再由线面平行的判定定理,得到结论
(2)取BC中点N,连接AN,可证得AN⊥平面BCDE,由(1)求出底面BCDE的面积S梯形BCDE,代入棱锥体积公式,可得答案.
(2)取BC中点N,连接AN,可证得AN⊥平面BCDE,由(1)求出底面BCDE的面积S梯形BCDE,代入棱锥体积公式,可得答案.
解答:证明:(1)取AC中点M,连接FM、BM,
∵F是AD中点,
∴FM∥DC,且FM=
DC=1,
∵EB⊥平面ABC,DC⊥平面ABC,
∴EB∥DC,
∴FM∥EB.
又∵EB=1,∴FM=EB,
∴四边形BEFM是平行四边形,
∴EF∥BM,
∵EF?平面ABC,BM?平面ABC,
∴EF∥平面ABC.
解:(2)取BC中点N,连接AN,
∵AB=AC,
∴AN=BC,
∵EB⊥平面ABC,
∴AN⊥EB,
∵BC与EB是底面BCDE内的相交直线,
∴AN⊥平面BCDE,
由(1)得,底面BCDE为直角梯形,S梯形BCDE=
=3,
在等边△ABC中,BC=2,
∴AN=
,
∴V棱锥A-BCDE=
S梯形BCDE•AN=
.
∵F是AD中点,
∴FM∥DC,且FM=
| 1 |
| 2 |
∵EB⊥平面ABC,DC⊥平面ABC,
∴EB∥DC,
∴FM∥EB.
又∵EB=1,∴FM=EB,
∴四边形BEFM是平行四边形,
∴EF∥BM,
∵EF?平面ABC,BM?平面ABC,
∴EF∥平面ABC.
解:(2)取BC中点N,连接AN,
∵AB=AC,
∴AN=BC,
∵EB⊥平面ABC,
∴AN⊥EB,
∵BC与EB是底面BCDE内的相交直线,
∴AN⊥平面BCDE,
由(1)得,底面BCDE为直角梯形,S梯形BCDE=
| ?EB+DC?•BC |
| 2 |
在等边△ABC中,BC=2,
∴AN=
| 3 |
∴V棱锥A-BCDE=
| 1 |
| 3 |
| 3 |
点评:本题考查的知识点是直线与平面平行的判定,棱锥的体积,熟练掌握线面平行的判定定理,线面垂直的性质定理和判定定理是解答的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目

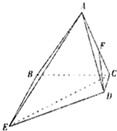 (2013•石家庄二模)如图,在四棱锥A-BCDE中,底面BCDE为直角梯形,且BE∥CD,CD⊥BC.侧面ABC⊥底面BCDE,F为AC的中点,BC=BE=4CD=2,AB=AC.
(2013•石家庄二模)如图,在四棱锥A-BCDE中,底面BCDE为直角梯形,且BE∥CD,CD⊥BC.侧面ABC⊥底面BCDE,F为AC的中点,BC=BE=4CD=2,AB=AC. (2012•海口模拟)四棱锥A-BCDE的正视图和俯视图如下,其中正视图是等边三角形,俯视图是直角梯形.
(2012•海口模拟)四棱锥A-BCDE的正视图和俯视图如下,其中正视图是等边三角形,俯视图是直角梯形.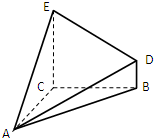 如图,四棱锥A-BCDE的底面BCDE是直角梯形,CE∥BD,∠ECB=90°,AC⊥平面BCDE,CE=CB=CA=2,BD=1.
如图,四棱锥A-BCDE的底面BCDE是直角梯形,CE∥BD,∠ECB=90°,AC⊥平面BCDE,CE=CB=CA=2,BD=1.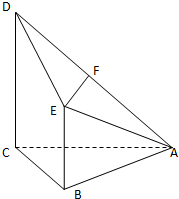 已知四棱锥A-BCDE,其中AB=BC=AC=BE=1,CD=2,CD⊥面ABC,BE∥CD,F为AD的中点.
已知四棱锥A-BCDE,其中AB=BC=AC=BE=1,CD=2,CD⊥面ABC,BE∥CD,F为AD的中点.