题目内容
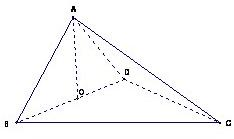 如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形,AB=2,AC=
如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形,AB=2,AC=| 6 |
(1)求证:AO⊥平面BCD;
(2)求二面角A-BC-D的余弦值.
分析:(1)欲证AO⊥平面BCD,根据直线与平面垂直的判定定理可知只需证AO与平面BCD内两相交直线垂直,连接OC,而AO⊥BD,AO⊥OC.∵BD∩OC=O,满足定理条件;
(2)过O作OE⊥BC于E,连接AE,根据二面角平面角的定义知∠AEO为二面角A-BC-D的平面角,在Rt△AEO中求出此角即可.
(2)过O作OE⊥BC于E,连接AE,根据二面角平面角的定义知∠AEO为二面角A-BC-D的平面角,在Rt△AEO中求出此角即可.
解答:解:(1)证明:连接OC,∵△ABD为等边三角形,O为BD的中点,
∴AO⊥BD.∵△ABD和△CBD为等边三角形,
O为BD的中点,AB=2,AC=
,
∴AO=CO=
.
在△AOC中,∵AO2+CO2=AC2,
∴∠AOC=90o,即AO⊥OC.∵BD∩OC=O,
∴AO⊥平面BCD.
(2)过O作OE⊥BC于E,连接AE,∵AO⊥平面BCD,
∴AE在平面BCD上的射影为OE.
∴AE⊥BC.∴∠AEO为二面角A-BC-D的平面角.
在Rt△AEO中,AO=
,OE=
,
tan∠AEO=
=2,
∴.cos∠AEO=
∴二面角A-BC-D的余弦值为
.
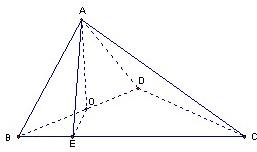
∴AO⊥BD.∵△ABD和△CBD为等边三角形,
O为BD的中点,AB=2,AC=
| 6 |
∴AO=CO=
| 3 |
在△AOC中,∵AO2+CO2=AC2,
∴∠AOC=90o,即AO⊥OC.∵BD∩OC=O,
∴AO⊥平面BCD.
(2)过O作OE⊥BC于E,连接AE,∵AO⊥平面BCD,
∴AE在平面BCD上的射影为OE.
∴AE⊥BC.∴∠AEO为二面角A-BC-D的平面角.
在Rt△AEO中,AO=
| 3 |
| ||
| 2 |
tan∠AEO=
| AO |
| OE |
∴.cos∠AEO=
| ||
| 5 |
| ||
| 5 |

点评:本小题主要考查直线与平面垂直的判定,以及二面角等基础知识,考查空间想象能力,运算能力和推理论证能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形,
如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形, 如图,四面体ABCD中,0是BD的中点,CA=CB=CD=BD=a,AB=AD=
如图,四面体ABCD中,0是BD的中点,CA=CB=CD=BD=a,AB=AD= 如图,四面体ABCD的各个面都是直角三角形,已知AB⊥BC,BC⊥CD,AB=a,BC=a,CD=c.
如图,四面体ABCD的各个面都是直角三角形,已知AB⊥BC,BC⊥CD,AB=a,BC=a,CD=c.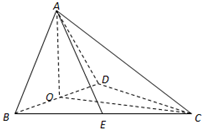 如图,四面体ABCD中,O、E分别是BD、BC的中点,AO⊥平面BCD,CA=CB=CD=BD=2.
如图,四面体ABCD中,O、E分别是BD、BC的中点,AO⊥平面BCD,CA=CB=CD=BD=2.