题目内容
如图所示,已知⊙O1与⊙O2相交于A,B两点,过点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1,⊙O2于点D,E,DE与AC相交于点P.
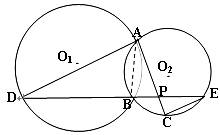
(1)求证:AD∥EC;
(2)若AD是⊙O2的切线,且PA=6,PC=2,BD=9,求AD的长.
解:(1)证明:连接AB,∵AC是⊙O1的切线,∴∠BAC=∠D,
又∵∠BAC=∠E,∴∠D=∠E。∴AD∥EC
(2)设BP=x,PE=y,∵PA=6,PC=2,∴xy=12,①
∵AD∥EC,∴![]() ②,
②,
由①②可得,![]() 或
或![]() (舍去)∴DE=9+x+y=16,
(舍去)∴DE=9+x+y=16,
∵AD是⊙O2的切线,
∴AD2=DB![]() DE=9×16,
DE=9×16,
∴AD=12。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
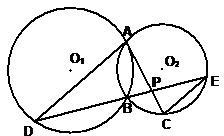 14、如图所示,已知⊙O1与⊙O2相交于A、B两点,过点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1、⊙O2于点D、E,DE与AC相交于点P.
14、如图所示,已知⊙O1与⊙O2相交于A、B两点,过点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1、⊙O2于点D、E,DE与AC相交于点P.
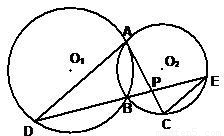 如图所示,已知⊙O1与⊙O2相交于A、B两点,过点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1、⊙O2于点D、E,DE与AC相交于点P.
如图所示,已知⊙O1与⊙O2相交于A、B两点,过点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1、⊙O2于点D、E,DE与AC相交于点P. 如图所示,已知⊙O1与⊙O2相交于A、B两点,过点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1、⊙O2于点D、E,DE与AC相交于点P.
如图所示,已知⊙O1与⊙O2相交于A、B两点,过点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1、⊙O2于点D、E,DE与AC相交于点P.