题目内容
在△ABC中,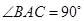 ,
,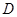 是
是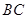 边的中点,
边的中点,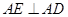 ,
, 交
交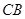 的延长线于
的延长线于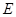 ,则下面结论中正确的是( )
,则下面结论中正确的是( )
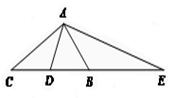
A.△AED∽△ACB B. △AEB∽△ACD
C. △BAE∽△ACE D. △AEC∽△DAC
【答案】
C
【解析】解:△BAE∽△ACE,因为两三角形除有公共角∠E外,
还有一锐角对应相等:因为∠BAC=90°,∠EAD=90°,所以∠BAE=∠DAC=∠ACE.
得到△BAE∽△ACE,
至于A,是两直角三角形,一般地∠ADE≠∠ABC;以及∠ADE>∠ACB,故不会相似;
再看B,是两钝角三角形,其钝角∠ABE=180°-∠ABD;钝角∠ADC=180°-∠ADB,
一般地∠ABD≠∠ADB,所以∠ABE≠∠ADC,故两三角形不会相似;
对于D,两三角形中△DAC是等腰三角形,而△AEC一般不是等腰三角形,故两三角形不会相似.
综上可知只有:△BAE∽△ACE,
故选C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=
如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
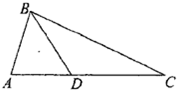 如图,在△ABC中,D是边AC上的点,且
如图,在△ABC中,D是边AC上的点,且