题目内容
设正项数列
的前项和为
，且
，
.
(1)求数列的通项公式；
(2)是否存在等比数列
，使
对一切正整数都成立？并证明你的结论.
（1）
解析:
(1)由 
得：
，
相减并整理得：
，
，即
是等差数列
，
(2)由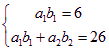
，解得：
猜想：
，使
成立
下面证明猜想成立：即证
对一切正整数都成立
令
，
则
两式相减得：
故原命题获证 .
练习册系列答案
相关题目
解析:
题目内容
设正项数列的前项和为 ，且，.
(1)求数列的通项公式；
(2)是否存在等比数列，使对一切正整数都成立？并证明你的结论.
（1）
(1)由 得：，
相减并整理得：
，，即
是等差数列
，
(2)由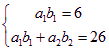，解得：
猜想：，使成立
下面证明猜想成立：即证对一切正整数都成立
令，
则
两式相减得：
故原命题获证 .
的前
项和为
，
为非零常数．已知对任意正整数
，当
时，
总成立．
成等差数列，求证：
≥
．
的前
项和为
且
求数列
的前
的前
项和为
，满足
，
．（Ⅰ）求数列
，证明：
的前
项和为
，满足
，
．
，证明：