Question

判断方程log₂x＋x²＝0在区间[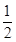，1]内有没有实数根？为什么？

 

Answer 1

【答案】

方程log₂x＋x²＝0在区间[，1]内有实根

【解析】解：设f(x)＝log₂x＋x²，

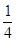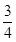∵f()＝log₂＋()²＝－1＋＝－＜0，

f(1)＝log₂1＋1＝1＞0，∴f()·f(1)＜0，函数f(x)＝log₂x＋x²的图象在区间[，1]上是连续的，因此，f(x)在区间[， 1]内有零点，即方程log₂x＋x²＝0在区间[，1]内有实根．