题目内容
(本小题满分12分)
有一块边长为4的正方形钢板,现对其切割、焊接成一个长方体无盖容器(切、焊损耗忽略不计).有人应用数学知识作如下设计:在钢板的四个角处各切去一个小正方形,剩余部分围成一个长方体,该长方体的高是小正方形的边长.
(1)请你求出这种切割、焊接而成的长方体容器的最大容积V1;
(2)请你判断上述方案是否是最佳方案,若不是,请设计一种新方案,使材料浪费最少,且所得长方体容器的容积V2>V1.
解:(1)设切去正方形边长为x,则焊接成的长方体的底面边长为4-2x,高为x,
∴V1=(4-2x)2x=4(x3-4x2+4x)(0<x<2). 2分
V′1=4(3x2-8x+4)=12(x-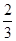 )(x-2).
4分
)(x-2).
4分
当0<x<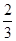 时,V′1>0;当
时,V′1>0;当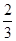 <x<2时,V′1<0.
6分
<x<2时,V′1<0.
6分
∴当x=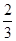 时,V1取最大值
时,V1取最大值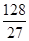 .
8分
.
8分
(2)重新设计方案如下:
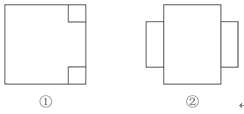
如图①,在正方形的两个角处各切下一个边长为1的小正方形;如图②,将切下的小正方形焊在未切口的正方形一边的中间;将图②焊成长方体容器.
新焊长方体容器底面是一长方形,长为3,宽为2,此长方体容积V2=3×2×1=6,显然V2>V1.故第二种方案符合要求. 12分
V1.故第二种方案符合要求. 12分
【解析】略

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案