题目内容
已知锐角α、β、γ满足:cos2α+cos2β+cos2γ=1,则tanαtanβtanγ的最小值为
______.
由cos2α+cos2β+cos2γ=1联想到锐角α、β、γ是长方体的对角线与过一个顶点的三条棱所成角,
记该长方体过一个顶点的三条棱长分别为a、b、c,
则tanαtanβtanγ=
•
•
≥
•
•
=2
,当且仅当a=b=c时,等号成立.
所以tanαtanβtanγ的最小值为2
.
故答案为2
记该长方体过一个顶点的三条棱长分别为a、b、c,
则tanαtanβtanγ=
| ||
| a |
| ||
| b |
| ||
| c |
| ||
| a |
| ||
| b |
| ||
| c |
| 2 |
所以tanαtanβtanγ的最小值为2
| 2 |
故答案为2
| 2 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 .其图象的两个相邻对称中心的距离为
.其图象的两个相邻对称中心的距离为 ,且过点
,且过点 .
. 的达式;
的达式; ,
,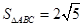 ,角C为锐角。且满
,角C为锐角。且满 ,求c的值.
,求c的值.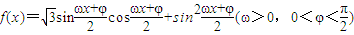 .其图象的两个相邻对称中心的距离为
.其图象的两个相邻对称中心的距离为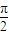 ,且过点
,且过点 .
.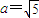 ,
,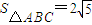 ,角C为锐角.且满
,角C为锐角.且满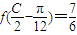 ,求c的值.
,求c的值. .其图象的两个相邻对称中心的距离为
.其图象的两个相邻对称中心的距离为 ,且过点
,且过点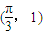 .
. ,
,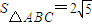 ,角C为锐角.且满
,角C为锐角.且满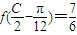 ,求c的值.
,求c的值.