题目内容
已知抛物线y2=2px(p>0),点P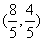 ,线段OP的垂直平分线经过抛物线的焦点F,经过F作两条互相垂直的弦AB、CD,设AB、CD的中点分别为M、N 。
,线段OP的垂直平分线经过抛物线的焦点F,经过F作两条互相垂直的弦AB、CD,设AB、CD的中点分别为M、N 。
(I)求抛物线的方程;
(II)直线MN是否经过定点?若经过,求出定点坐标;若不经过,试说明理由。
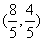 ,线段OP的垂直平分线经过抛物线的焦点F,经过F作两条互相垂直的弦AB、CD,设AB、CD的中点分别为M、N 。
,线段OP的垂直平分线经过抛物线的焦点F,经过F作两条互相垂直的弦AB、CD,设AB、CD的中点分别为M、N 。(I)求抛物线的方程;
(II)直线MN是否经过定点?若经过,求出定点坐标;若不经过,试说明理由。
解:(Ⅰ)由P(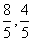 ),O(0,0),
),O(0,0),
∴kOP=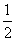 ,OP的中点为
,OP的中点为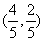 ,
,
∴OP的垂直平分线所在直线方程y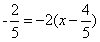 ,即2x+y-2=0。
,即2x+y-2=0。
令y=0,解得:x=1,
故得:p=2,
∴抛物线方程为:y2=4x。
(Ⅱ)假设直线MN过定点,
设A(xA,yA),B (xB,yB),M(xM,yM),
设直线AB的斜率为k,则直线AB的方程为y=k(x-1),
联立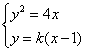 ,可得:k2x2-(2k2+4)x+k2=0,
,可得:k2x2-(2k2+4)x+k2=0,
由韦达定理,得xA+xB=2+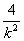 ,
,
所以,xM=1+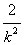 ,
,
所以,点M的坐标是(1+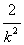 ,-2k),
,-2k),
当k≠±1时,
直线MN的斜率为: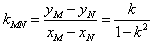 ,
,
直线方程为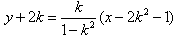 ,
,
整理得:y(1-k2)=k(x-3),
∴直线恒经过定点(3,0),
当k=±1时,直线MN方程为x=3,经过(3,0),
综上,不论k为何值,直线MN恒过定点(3,0)。
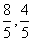 ),O(0,0),
),O(0,0), ∴kOP=
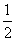 ,OP的中点为
,OP的中点为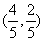 ,
,∴OP的垂直平分线所在直线方程y
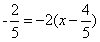 ,即2x+y-2=0。
,即2x+y-2=0。 令y=0,解得:x=1,
故得:p=2,
∴抛物线方程为:y2=4x。
(Ⅱ)假设直线MN过定点,
设A(xA,yA),B (xB,yB),M(xM,yM),
设直线AB的斜率为k,则直线AB的方程为y=k(x-1),
联立
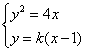 ,可得:k2x2-(2k2+4)x+k2=0,
,可得:k2x2-(2k2+4)x+k2=0,由韦达定理,得xA+xB=2+
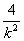 ,
,所以,xM=1+
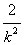 ,
,所以,点M的坐标是(1+
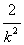 ,-2k),
,-2k),当k≠±1时,
直线MN的斜率为:
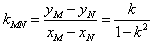 ,
,直线方程为
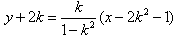 ,
,整理得:y(1-k2)=k(x-3),
∴直线恒经过定点(3,0),
当k=±1时,直线MN方程为x=3,经过(3,0),
综上,不论k为何值,直线MN恒过定点(3,0)。

练习册系列答案
相关题目