题目内容
已知等差数列 ,公差
,公差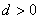 ,前n项和为
,前n项和为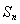 ,
,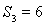 ,且满足
,且满足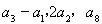 成等比数列.
成等比数列.
(I)求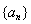 的通项公式;
的通项公式;
(II)设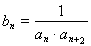 ,求数列
,求数列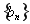 的前
的前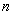 项和
项和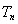 的值.
的值.
【答案】
(1)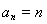 ;(2)
;(2)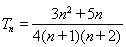 .
.
【解析】
试题分析:本题主要考查等差数列的通项公式、等差数列的性质、等比中项以及裂项相消法求和等数学知识,考查基本运算能力.第一问,利用等差数列的性质得到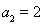 ,再利用等比中项得
,再利用等比中项得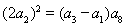 ,
,
利用等差数列的通项公式展开求出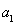 和
和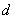 ,所以可以写出数列的通项公式;第二问,将第一问的结论代入,将
,所以可以写出数列的通项公式;第二问,将第一问的结论代入,将 化简,得到
化简,得到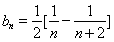 ,将每一项都用这种形式展开,数列求和.
,将每一项都用这种形式展开,数列求和.
试题解析:(I)由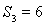 ,得
,得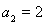
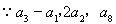 成等比数列 ,
成等比数列 ,
 ,
,
解得: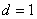 或
或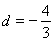 , 3分
, 3分
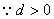
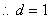
 数列
数列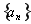 的通项公式为
的通项公式为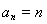 . 5分
. 5分
(Ⅱ)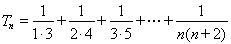
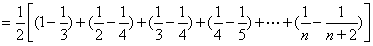
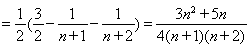 10分
10分
考点:1.等比中项;2.等差数列的性质;3.等差数列的通项公式;4.裂项相消法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 的公差为
的公差为 ,项数是偶数,所有奇数项之和为
,项数是偶数,所有奇数项之和为 ,所有偶数项之和为
,所有偶数项之和为 ,则这个数列的项数为 ;
,则这个数列的项数为 ;