题目内容
过点Q  作圆C:x2+y2=r2(
作圆C:x2+y2=r2( )的切线,切点为D,且QD=4.
)的切线,切点为D,且QD=4.
(1)求r的值;
(2)设P是圆C上位于第一象限内的任意一点,过点P作圆C的切线l,且l交x轴于点A,交y 轴于点B,设 ,求
,求 的最小值(O为坐标原点).
的最小值(O为坐标原点).
(1)圆C:x2+y2=r2( )的圆心为O(0,0),于是
)的圆心为O(0,0),于是
由题设知, 是以D为直角顶点的直角三角形,
是以D为直角顶点的直角三角形,
故有 …………4分
…………4分
(2)解法一:
设直线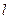 的方程为
的方程为 即
即
则


 直线
直线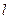 与圆C相切
与圆C相切


当且仅当 时取到“=”号
时取到“=”号 取得最小值为6。
取得最小值为6。
解法二:
设P(x0,y0)( ),则
),则 ,
,
且直线l的方程为 . …………6分
. …………6分
令y=0,得x= ,即
,即 ,
,
令x=0,得y= ,即
,即 .
.
于是
 . …………8分
. …………8分
因为 , 且
, 且 ,所以
,所以 …………9分
…………9分
所以 ………11分
………11分
当且仅当 时取“=”号.
时取“=”号.
故当 时,
时, 取得最小值6. …………12分
取得最小值6. …………12分
解析

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
 作圆C:x2+y2=r2(
作圆C:x2+y2=r2( )的切线,切点为D,且QD=4.
)的切线,切点为D,且QD=4. ,求
,求 的最小值(O为坐标原点).
的最小值(O为坐标原点). 作圆O:x2+y2=r2(r>0)的切线,切点为D,且QD=4.
作圆O:x2+y2=r2(r>0)的切线,切点为D,且QD=4.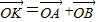 ,求
,求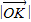 的最小值(O为坐标原点).
的最小值(O为坐标原点).