题目内容
直线y=k(x-a)+1与椭圆 总有公共点,则实数a的取值范围是
总有公共点,则实数a的取值范围是
- A.[-2,2]
- B.[-1,1]
- C.

- D.
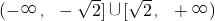
C
分析:由于直线恒过定点(a,1)要使直线y=k(x-a)+1与椭圆 总有公共点,则必须定点在椭圆内或椭圆上,从而可建立不等关系,进而可求实数a的取值范围.
总有公共点,则必须定点在椭圆内或椭圆上,从而可建立不等关系,进而可求实数a的取值范围.
解答:由题意,直线恒过定点(a,1)
要使直线y=k(x-a)+1与椭圆 总有公共点,则必须定点在椭圆内或椭圆上
总有公共点,则必须定点在椭圆内或椭圆上
∴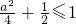
∴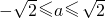
故选C.
点评:本题以直线与椭圆的位置关系为载体,考查直线与椭圆恒由公共点,解题的关键是巧妙利用直线恒过定点,从而转化为点与椭圆的位置关系.
分析:由于直线恒过定点(a,1)要使直线y=k(x-a)+1与椭圆
 总有公共点,则必须定点在椭圆内或椭圆上,从而可建立不等关系,进而可求实数a的取值范围.
总有公共点,则必须定点在椭圆内或椭圆上,从而可建立不等关系,进而可求实数a的取值范围.解答:由题意,直线恒过定点(a,1)
要使直线y=k(x-a)+1与椭圆
 总有公共点,则必须定点在椭圆内或椭圆上
总有公共点,则必须定点在椭圆内或椭圆上∴
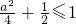
∴
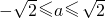
故选C.
点评:本题以直线与椭圆的位置关系为载体,考查直线与椭圆恒由公共点,解题的关键是巧妙利用直线恒过定点,从而转化为点与椭圆的位置关系.

练习册系列答案
相关题目
 总有公共点,则实数a的取值范围是( )
总有公共点,则实数a的取值范围是( )
