题目内容
设正四面体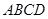 的棱长为
的棱长为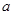 ,
,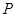 是棱
是棱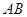 上的任意一点,且
上的任意一点,且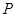 到面
到面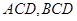 的距离分别为
的距离分别为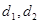 ,则
,则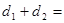 ___ .
___ .
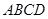 的棱长为
的棱长为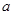 ,
,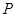 是棱
是棱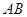 上的任意一点,且
上的任意一点,且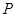 到面
到面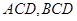 的距离分别为
的距离分别为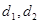 ,则
,则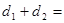 ___ .
___ .
试题分析:根据题意,由于正四面体
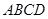 的棱长为
的棱长为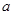 ,各个面的面积为
,各个面的面积为 ,高为
,高为 ,那么可知底面积乘以高的三分之一即为四面体的体积,也等于从点P出发的两个棱锥的体积和且底面积相同,因此可知高为
,那么可知底面积乘以高的三分之一即为四面体的体积,也等于从点P出发的两个棱锥的体积和且底面积相同,因此可知高为
点评:主要是考查了等体积法的运用,属于基础题。

练习册系列答案
相关题目
题目内容
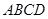 的棱长为
的棱长为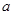 ,
,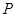 是棱
是棱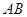 上的任意一点,且
上的任意一点,且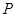 到面
到面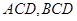 的距离分别为
的距离分别为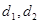 ,则
,则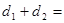 ___ .
___ .
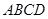 的棱长为
的棱长为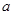 ,各个面的面积为
,各个面的面积为 ,高为
,高为 ,那么可知底面积乘以高的三分之一即为四面体的体积,也等于从点P出发的两个棱锥的体积和且底面积相同,因此可知高为
,那么可知底面积乘以高的三分之一即为四面体的体积,也等于从点P出发的两个棱锥的体积和且底面积相同,因此可知高为
