题目内容
函数f(x)=|sinπx-cosπx|对任意的x∈R都有f(x1)≤f(x)≤f(x2)成立,则|x2-x1|的最小值为( )
分析:先将函数写出分段函数,再确定|x2-x1|的最小值为相邻最小值与最大值处横坐标差的绝对值,数形结合可得结论.
解答: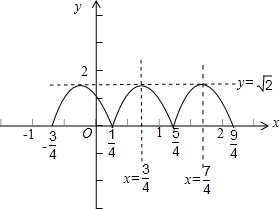 解:由题意,f(x)=|sinπx-cosπx|=|
解:由题意,f(x)=|sinπx-cosπx|=|
(
sinπx-
cosπx)|=
|sin(πx-
)|,
它的周期为
×
=1,最大值为
,最小值为0,f(x)的图象如图所示:
∵对任意的x∈R都有f(x1)≤f(x)≤f(x2)成立,所以f(x1)是最小值,f(x2)是最大值.
|x2-x1|的最小值为相邻最小值与最大值处横坐标差的绝对值.
结合图形可得,当x=
时,函数取得最小值0,x=
时,函数取得最大值为
,
且此时|x2-x1|取得最小值为
-
=
,
故选 D.
 解:由题意,f(x)=|sinπx-cosπx|=|
解:由题意,f(x)=|sinπx-cosπx|=|| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| π |
| 4 |
它的周期为
| 1 |
| 2 |
| 2π |
| π |
| 2 |
∵对任意的x∈R都有f(x1)≤f(x)≤f(x2)成立,所以f(x1)是最小值,f(x2)是最大值.
|x2-x1|的最小值为相邻最小值与最大值处横坐标差的绝对值.
结合图形可得,当x=
| 1 |
| 4 |
| 3 |
| 4 |
| 2 |
且此时|x2-x1|取得最小值为
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
故选 D.
点评:本题考查绝对值函数,考查三角函数的性质,确定|x2-x1|的最小值为相邻最小值与最大值处横坐标差的绝对值是关键,
属于中档题.
属于中档题.

练习册系列答案
相关题目
下列命题中是假命题的是( )
| A、?m∈R,使f(x)=(m-1)•xm2-4m+3是幂函数,且在(0,+∞)上递减 | B、?a>0,函数f(x)=ln2x+lnx-a有零点 | C、?α,β∈R,使cos(α+β)=cosα+sinβ | D、?φ∈R,函数f(x)=sin(2x+φ)都不是偶函数 |
 若函数f(x)=sin(ωx+?)的部分图象如图所示,则ω和?的值可以是( )
若函数f(x)=sin(ωx+?)的部分图象如图所示,则ω和?的值可以是( )