题目内容
(本小题共13分)
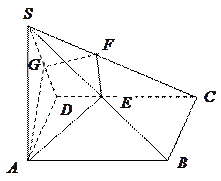
如图,在四棱锥P—ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠ABC=
∠BAD=90°,AD>BC,E,F分别为棱AB,PC的中点.
(I)求证:PE⊥BC;
(II)求证:EF//平面PAD.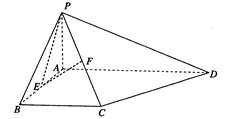
如图,在四棱锥P—ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠ABC=
∠BAD=90°,AD>BC,E,F分别为棱AB,PC的中点.
(I)求证:PE⊥BC;
(II)求证:EF//平面PAD.

(I)证明见解析。
(II)证明见解析。
(II)证明见解析。
证明:(I)
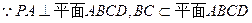
∴PA⊥BC
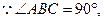
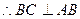
∴BC⊥平面PAB
又E是AB中点,
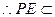 平面PAB
平面PAB∴BC⊥PE. …………6分
(II)证明:取CD中点G,连结FG,EG,
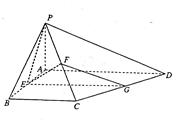
∵F为PC中点,∴FG//PD
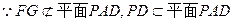
∴FG//平面PAD;
同理,EG//平面PAD
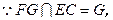
∴平面EFG//平面PAD.
∴EF//平面PAD. …………13分

练习册系列答案
相关题目
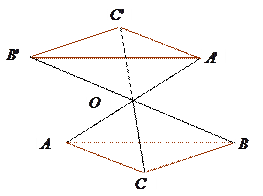
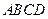 中,
中,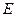 是
是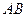 的中点,点
的中点,点 是
是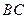 的中点,将
的中点,将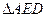 ,
,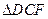 分别沿
分别沿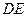 ,
,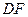 折起,使
折起,使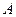 ,
,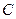 两点重合于点
两点重合于点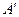 .求证:
.求证: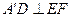 .
.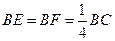 时,求三棱椎
时,求三棱椎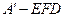 的体积.
的体积.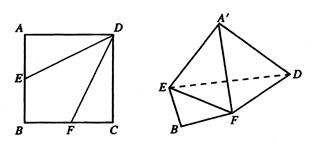
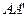 ,
,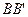 ,
,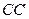 相交于
相交于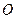 ,
,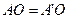 ,
,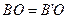 ,
, .
.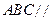 平面
平面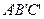 .
.
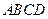 为正方形,
为正方形,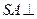 平面
平面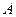 且垂直于
且垂直于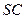 的平面分别交
的平面分别交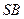 ,
,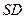 于
于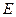 ,
,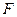 ,
,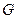 .求证:
.求证: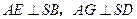 .
.
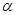 的斜线
的斜线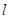 与平面
与平面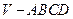 中,底面
中,底面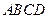 是正方形,侧面
是正方形,侧面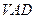 是正三角形,平面
是正三角形,平面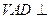 底面
底面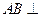 平面
平面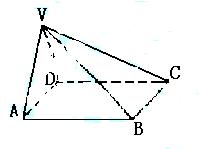
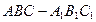 是各棱长为5的正三棱柱,
是各棱长为5的正三棱柱,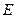 ,
,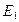 分别是
分别是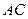 ,
,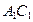 的中点,则平面
的中点,则平面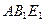 与平面
与平面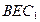 的距离为多少
的距离为多少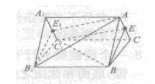
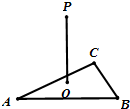
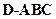 的外接球的球心O满足
的外接球的球心O满足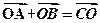 ,且外接球的体积为
,且外接球的体积为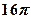 ,则该三棱锥的体积为 .
,则该三棱锥的体积为 .