题目内容
已知若
=(-2,λ),
=(3,-5),
和
夹角为钝角,则λ的取值范围是( )
| a |
| b |
| a |
| b |
分析:两个不共线向量夹角为钝角的充分必要条件是它们的数量积小于零.由此可根据数量积的公式,列出不等式组,可得到实数λ的取值范围.
解答:解:
=(-2,λ),
=(3,-5),
和
夹角为钝角,
所以
•
<0,且
,
不共线,即
解得λ∈(-
,
)∪(
,+∞)
故选C
| a |
| b |
| a |
| b |
所以
| a |
| b |
| a |
| b |
|
解得λ∈(-
| 6 |
| 5 |
| 10 |
| 3 |
| 10 |
| 3 |
故选C
点评:本题考查向量的数量积的应用,考查计算能力,解题的关键是理解夹角为钝角与数量积为负的对应关系,由夹角为钝角可得出两向量内积小于0,由数量积小于0不一定能得出两向量夹角为钝角.

练习册系列答案
相关题目
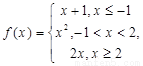 若
若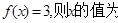 A. 2 B. 2或
A. 2 B. 2或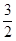 C.
C. 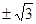 D.
D.