题目内容
设O是坐标原点,A、B、C是坐标平面上的三个不同点,若 ,
,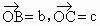 .
.
求证:若A、B、C三点共线,则存在三个全不为0的实数l、m、n使la+mb+nc=0.且l+m+n=0.
答案:略
解析:
提示:
解析:
|
证明:∵ A、B、C三点共线,∴存在实数l ,使 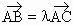 ,即b-a=l
(c-a). ,即b-a=l
(c-a).
∴ (l -1)a+b-l c=0.令 l=l -1,m=1,n=-l ,此时l+m+n=0. |
提示:
|
(1)通过本题学会把三点共线问题转化为两向量的共线问题,根据向量共线的条件去解决. (2)请同学们思考:若存在三个全不为0的实数l、m、n使la+mb+nc=0,且l+m+n=0,问A、B、C三点是否共线? |

练习册系列答案
相关题目
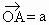 ,
,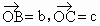 .
.