题目内容
选做题(考生只能从中选做一题)(1)(坐标系与参数方程选做题)曲线
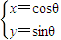 (θ为参数)上的点到两坐标轴的距离之和的最大值是 .
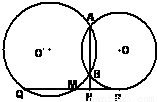
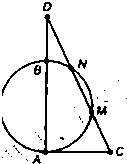
(θ为参数)上的点到两坐标轴的距离之和的最大值是 .(2)(几何证明选讲选做题)如右图,⊙O′和⊙O相交于A和B,PQ切⊙O于P,交⊙O′于Q和M,交AB的延长线于N,MN=3,NQ=15,则 PN= .
【答案】分析:(1)利用参数方程直接表示出点到两坐标轴的距离之和|sinx|+|cosx|,然后变形求解,再利用三角函数的有界性求最值.
(2)根据PM是⊙O的切线,MA是⊙O的割线,得到切割线定理,NA是⊙O′的割线,NQ是⊙O′的割线,得到割线定理,根据等量代换,得到结果
解答:解:(1)曲线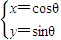 (θ为参数)上的点到两坐标轴的距离之和为:
(θ为参数)上的点到两坐标轴的距离之和为:
d=|sinθ|+|cosθ|=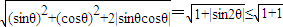 =
=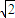 ,
,
故答案为: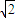 .
.
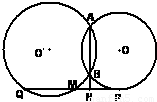 (2)∵PM是⊙O的切线,NA是⊙O的割线
(2)∵PM是⊙O的切线,NA是⊙O的割线
∴PN2=NB•NA
∵NA是⊙O′的割线
NQ是⊙O′的割线
∴NM•NQ=NB•NA,
∴PN2=NM•NQ,
∵MN=3,NQ=15
∴PN=3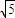
故答案为:3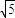 .
.
点评:本题主要考查了圆的参数方程,以及研究距离和的最值问题,还考查与圆有关的比例线段,(2)题解题的关键是利用等量代换做出要用的关系式,代入数据得到结果.属于基础题.
(2)根据PM是⊙O的切线,MA是⊙O的割线,得到切割线定理,NA是⊙O′的割线,NQ是⊙O′的割线,得到割线定理,根据等量代换,得到结果
解答:解:(1)曲线
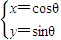 (θ为参数)上的点到两坐标轴的距离之和为:
(θ为参数)上的点到两坐标轴的距离之和为:d=|sinθ|+|cosθ|=
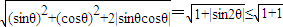 =
=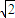 ,
,故答案为:
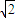 .
. (2)∵PM是⊙O的切线,NA是⊙O的割线
(2)∵PM是⊙O的切线,NA是⊙O的割线∴PN2=NB•NA
∵NA是⊙O′的割线
NQ是⊙O′的割线
∴NM•NQ=NB•NA,
∴PN2=NM•NQ,
∵MN=3,NQ=15
∴PN=3
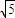
故答案为:3
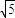 .
.点评:本题主要考查了圆的参数方程,以及研究距离和的最值问题,还考查与圆有关的比例线段,(2)题解题的关键是利用等量代换做出要用的关系式,代入数据得到结果.属于基础题.

练习册系列答案
相关题目
 选做题(这里给出了3道选做题,考生只能从中选做一题,多答时按顺序只评第1位置题)
选做题(这里给出了3道选做题,考生只能从中选做一题,多答时按顺序只评第1位置题) 选做题(考生只能从中选做一题)
选做题(考生只能从中选做一题) 与圆
与圆 的位置关系是 。
的位置关系是 。 且
且 则
则 ;
;  , 则
, 则 ;
; 则
则 ;
; 则
则 的最小值为8.其中是真命题的序号是_______________。
的最小值为8.其中是真命题的序号是_______________。 与圆
与圆 的位置关系是 。
的位置关系是 。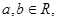 且
且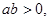 则
则 ;
;  , 则
, 则 ;
; 则
则 ;
; 则
则 的最小值为8.其中是真命题的序号是_______________。
的最小值为8.其中是真命题的序号是_______________。