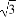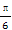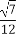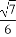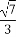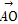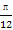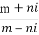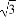题目内容
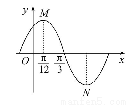
若函数f(x)=(sinx+cosx)2-2cos2x-m在[0,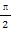
]上有零点,则实数m的取值范围为( )
(A)[-1,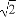
] (B)[-1,1]
(C)[1,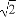] (D)[-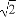,-1]
A
【解析】f(x)=(sinx+cosx)2-2cos2x-m
=1+sin 2x-2cos2x-m
=1+sin 2x-1-cos 2x-m
=
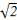sin(2x-
)-m.
∵0≤x≤
,∴0≤2x≤π,∴-≤2x-≤
,
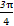∴-1≤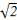sin(2x-)≤,
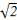故当-1≤m≤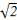时,f(x)在[0,]上有零点.
练习册系列答案
相关题目
