题目内容
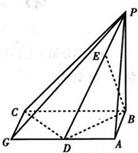 已知四棱锥中P-ABCG中,底面ABCG是矩形,D为AG的中点,BC=2AB=2,又PB⊥平面ABCG,且PB=1,点E在棱PD上,且DE=2PE
已知四棱锥中P-ABCG中,底面ABCG是矩形,D为AG的中点,BC=2AB=2,又PB⊥平面ABCG,且PB=1,点E在棱PD上,且DE=2PE
(Ⅰ)求异面直线PA与CD所成的角的大小;
(Ⅱ)求证:BE⊥平面PCD.
解:(Ⅰ)取BC中点F,连接AF,则CF=AD且CF∥AD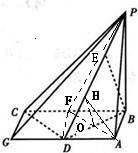
∴四边形ADCF是平行四边形?AF∥CD
∴∠PAF(或其补角)为异面直线PA、CD所成的角
∵PB⊥平面ABCG,BA、BF是平面ABCG内的直线
∴PB⊥BA,PB⊥BF
∵PB=AB=BF=1,AB⊥BC
∴PA=PF=AF= ?△PAF是等边三角形,∠PAF=60°
?△PAF是等边三角形,∠PAF=60°
∴异面直线PA与CD所成的角为60°
(II)由(I)知,CF=BF=DF
∴∠CDB=90°?CD⊥BD
又∵PB⊥平面DBC?PB⊥CD
∵PB∩BD=B
∴CD⊥平面BDP?CD⊥BE
在Rt△PBD中,PB=1、BD=
∴
∵DE=2PE,得
∴ ?△PBE∽△PDB
?△PBE∽△PDB
∴BE⊥PD
∵CD∩PD=D
∴BE⊥平面PCD
分析:(I)取BC中点F,连接AF,可以证出四边形ADCF是平行四边形,得到CD与AF互相平行,从而得到AF与PA所成的直角或锐角就是异面直线PA与CD所成的角,再利用垂直关系和已知的线段长可计算出△PAF是等边三角形,故异面直线PA与CD所成的角为60°;
(II)利用中线等于一边的一半证明出CD⊥BD,结合CD⊥PB得到CD⊥平面PBD,从而CD⊥BE.再在Rt△PBD中利用已知线段的长可以算出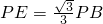 ,从而利用相似三角形证出BE⊥PD,结合线面垂直的判定定理,得到BE⊥平面PCD.
,从而利用相似三角形证出BE⊥PD,结合线面垂直的判定定理,得到BE⊥平面PCD.
点评:本题是一道立体几何的综合题,着重考查了直线与平面垂直的判定和异面直线及其所成的角等知识点,属于中档题.

∴四边形ADCF是平行四边形?AF∥CD
∴∠PAF(或其补角)为异面直线PA、CD所成的角
∵PB⊥平面ABCG,BA、BF是平面ABCG内的直线
∴PB⊥BA,PB⊥BF
∵PB=AB=BF=1,AB⊥BC
∴PA=PF=AF=
 ?△PAF是等边三角形,∠PAF=60°
?△PAF是等边三角形,∠PAF=60°∴异面直线PA与CD所成的角为60°
(II)由(I)知,CF=BF=DF
∴∠CDB=90°?CD⊥BD
又∵PB⊥平面DBC?PB⊥CD
∵PB∩BD=B
∴CD⊥平面BDP?CD⊥BE
在Rt△PBD中,PB=1、BD=

∴

∵DE=2PE,得

∴
 ?△PBE∽△PDB
?△PBE∽△PDB∴BE⊥PD
∵CD∩PD=D
∴BE⊥平面PCD
分析:(I)取BC中点F,连接AF,可以证出四边形ADCF是平行四边形,得到CD与AF互相平行,从而得到AF与PA所成的直角或锐角就是异面直线PA与CD所成的角,再利用垂直关系和已知的线段长可计算出△PAF是等边三角形,故异面直线PA与CD所成的角为60°;
(II)利用中线等于一边的一半证明出CD⊥BD,结合CD⊥PB得到CD⊥平面PBD,从而CD⊥BE.再在Rt△PBD中利用已知线段的长可以算出
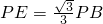 ,从而利用相似三角形证出BE⊥PD,结合线面垂直的判定定理,得到BE⊥平面PCD.
,从而利用相似三角形证出BE⊥PD,结合线面垂直的判定定理,得到BE⊥平面PCD.点评:本题是一道立体几何的综合题,着重考查了直线与平面垂直的判定和异面直线及其所成的角等知识点,属于中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
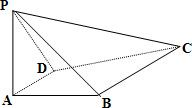 如图,已知四棱锥P-ABCD中,PA⊥平面CDAB,ABCD是直角梯形,AD∥BC,∠BAD=90°,BC=2,PA=AB=1.求点D到平面PBC的距离.
如图,已知四棱锥P-ABCD中,PA⊥平面CDAB,ABCD是直角梯形,AD∥BC,∠BAD=90°,BC=2,PA=AB=1.求点D到平面PBC的距离.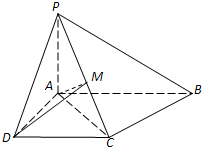 如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.
如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.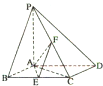 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点. 已知四棱锥P-ABCD中,点M是PC的中点,点E是AB上的一个动点,且该四棱锥的三视图如图所示,其中正视图和侧视图是直角三角形.
已知四棱锥P-ABCD中,点M是PC的中点,点E是AB上的一个动点,且该四棱锥的三视图如图所示,其中正视图和侧视图是直角三角形.