题目内容
已知数列{an}的通项为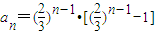
，下列表述正确的是（ ）A．最大项为0，最小项为
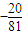
B．最大项为0，最小项不存在
C．最大项不存在，最小项为
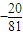
D．最大项为0，最小项为a4
【答案】分析：先求出数列的前四项，然后计算an+1-an的符号，从而确定数列的单调性，即可求出数列的最大值和最小值．
解答：解：a1=（
）1-1×[（
）1-1-1]=1×（1-1）=0
∵当n＞1时，（
）n-1＜1，（
）n-1-1＜0
∴an最大项为a1=0
a2=（
）2-1×[（
）2-1-1]=
×（
-1）=-
a3=（
）3-1×[（
）3-1-1]=
×（
-1）=-
a4=（
）4-1×[（
）4-1-1]=
×（
-1）=-
an+1-an=（
）n+1-1×[（
）n+1-1-1]-（
）n-1×[（
）n-1-1]
=（
）n-1×
当n≥3时，an+1-an＞0
n＜3时 an+1-an＜0
最小项为a3=-
故选A．
点评：本题主要考查了数列的函数特性，同时考查了计算能力，属于中档题．
解答：解：a1=（
）1-1×[（）1-1-1]=1×（1-1）=0∵当n＞1时，（
）n-1＜1，（）n-1-1＜0 ∴an最大项为a1=0
a2=（
）2-1×[（）2-1-1]=×（-1）=-a3=（
）3-1×[（）3-1-1]=×（-1）=-a4=（
）4-1×[（）4-1-1]=×（-1）=-an+1-an=（
）n+1-1×[（）n+1-1-1]-（）n-1×[（）n-1-1]=（
）n-1×当n≥3时，an+1-an＞0
n＜3时 an+1-an＜0
最小项为a3=-
故选A．
点评：本题主要考查了数列的函数特性，同时考查了计算能力，属于中档题．
练习册系列答案
相关题目
已知数列{an}的通项为an=2n-1，Sn为数列{an}的前n项和，令bn=
，则数列{bn}的前n项和的取值范围为（ ）
| 1 |
| Sn+n |
A、[
| ||||
B、(
| ||||
C、[
| ||||
D、[
|