题目内容
(1)解不等式
≥3;
(2)a,b∈R+,2c>a+b,求证c-
<a<c+
.
| 2x2-4x-1 |
| x2-2x-3 |
(2)a,b∈R+,2c>a+b,求证c-
| c2-ab |
| c2-ab |
(1)原不等式等价于
≥0,即
≤0,
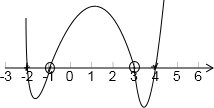
由穿根法(并验根)求得 x∈[-2,-1)∪(3,4].
(2)要证原式成立,即证-
<a<c<
,即证|a-c|<
,即证|a-c|2<(
)2,
即证a2-2ac+c2<c2-ab,即证a2+ab>2ac,即证a+b<2c,由题设,此式成立,
∴原命题成立.
| -x2+2x+8 |
| x2-2x-3 |
| (x-4)(x+2) |
| (x-3)(x+1) |
由穿根法(并验根)求得 x∈[-2,-1)∪(3,4].

(2)要证原式成立,即证-
| c2-ab |
| c2-ab |
| c2-ab |
| c2-ab |
即证a2-2ac+c2<c2-ab,即证a2+ab>2ac,即证a+b<2c,由题设,此式成立,
∴原命题成立.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 ≥9;
≥9; ≥
≥ .
.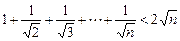 (n∈N*)
(n∈N*)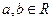 ,求证:
,求证: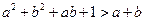
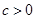 ,整数
,整数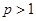 ,
,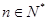 .
.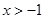 且
且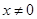 时,
时,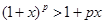 ;
;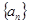 满足
满足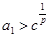 ,
,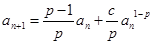 ,证明:
,证明: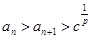 .
.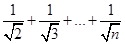 n∈N?),g(n)=2(
n∈N?),g(n)=2(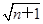 -1)(n∈N?).
-1)(n∈N?). ,求证:
,求证: 。
。