题目内容
已知奇函数
的定义域为R，且在
上是增函数，是否存在实数
，使
对所有
都成立？若存在，求出符合条件的所有实数的范围，若不存在，说明理由
解：∵
是
上的奇函数，且在
上是增函数
∴是上的增函数，于是不等式可等价地转化为：
即
，即
方法一：对于
恒成立等价于
对于恒成立
∵当时，
∴
方法二：设
，则问题等价地转化为函数
在
上的值恒为正
又转化为函数
在上的最小值为正
当
，即
时，
与不符
当
时，即
时，
∴
当
，即
时，
∴
综上：
的值存在，其取值是
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
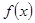的定义域为实数集
，且
上是增函数，当
时，是否存在实数
，使
对所有的
恒成立？若存在，求出实数
的定义域为
，且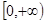
上是增函数, 是否存在实数
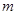使得
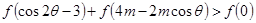, 对一切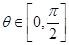
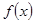的定义域为
，且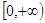
上是增函数, 是否存在实数
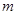使得
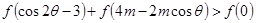, 对一切
都成立？若存在，求出实数
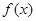的定义域为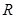
，且是以2为周期的周期函数，数列
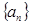是首项为1，公差为1的等差数列，则
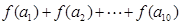的值为 （ ）
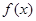的定义域为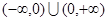
，且在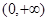
上为增函数，
.
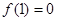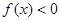的解集；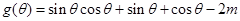
，
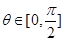，若不等式组
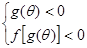恒成立，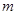
的取值范围.