题目内容
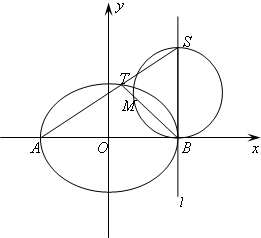 如图,已知曲线C:
如图,已知曲线C:| x2 |
| a2 |
(I)若点T与点M重合,求
| AT |
| AS |
(II)若点O、M、S三点共线,求曲线C的方程.
分析:(I)设T(x0,y0),S(a,y1),由点A,T,S共线,确定直线方程,求得S的坐标,利用点T与点M重合时,有BT⊥AS,kSA•kBT=-1,得a的值,再利用
•
=AB2,即可求得结论;
(II)以线段SB为直径的圆相交于点M点,又O、M、S三点共线,知BM⊥OS,∴BT⊥OS,由此可求a的值,从而可得曲线C的方程.
| AT |
| AS |
(II)以线段SB为直径的圆相交于点M点,又O、M、S三点共线,知BM⊥OS,∴BT⊥OS,由此可求a的值,从而可得曲线C的方程.
解答:解:(I)设T(x0,y0),S(a,y1),则
+y02=1,所以y02=1-
由点A,T,S共线有:
=
,得:y1=
y0,即S(a,
y0)
当点T与点M重合时,有BT⊥AS,kSA•kBT=
×
=-1,得a=1.
∴
•
=AB2=(2a)2=4;
(II)以线段SB为直径的圆相交于点M点,又O、M、S三点共线,知BM⊥OS,∴BT⊥OS
∴kSO•kBT=
×
=-1,∴a2=2
∴所求曲线C的方程为
+y2=1.
| x02 |
| a2 |
| x02 |
| a2 |
由点A,T,S共线有:
| y0-0 |
| x0+a |
| y1-0 |
| a+a |
| 2a |
| x0+a |
| 2a |
| x0+a |
当点T与点M重合时,有BT⊥AS,kSA•kBT=
| y0 |
| x0+a |
| y0 |
| x0-a |
∴
| AT |
| AS |
(II)以线段SB为直径的圆相交于点M点,又O、M、S三点共线,知BM⊥OS,∴BT⊥OS
∴kSO•kBT=
| ||
| a |
| y0 |
| x0-a |
∴所求曲线C的方程为
| x2 |
| 2 |
点评:本题考查椭圆的标准方程,考查向量知识的运用,解题的关键是确定a的值,属于中档题.

练习册系列答案
相关题目
 如图,已知曲线
如图,已知曲线
 如图,已知曲线C:
如图,已知曲线C: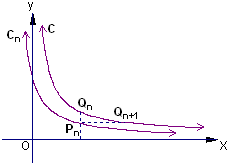 如图,已知曲线C:
如图,已知曲线C: 如图:已知曲线C:在点P(1,1)处的切线与x轴交于点Q1,再过Q1点作x轴的垂线交曲线C于点P1,再过P1作C的切线与x轴交于点Q2,依次重复下去,过Pn(xn,yn)作C的切线与x轴交于点Qn(xn+1,O).
如图:已知曲线C:在点P(1,1)处的切线与x轴交于点Q1,再过Q1点作x轴的垂线交曲线C于点P1,再过P1作C的切线与x轴交于点Q2,依次重复下去,过Pn(xn,yn)作C的切线与x轴交于点Qn(xn+1,O).