题目内容
若关于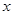 的不等式
的不等式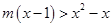 的解集为
的解集为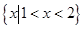 ,则实数
,则实数 的值为 .
的值为 .
【答案】
2
【解析】
试题分析: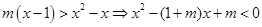 ,解集为
,解集为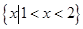 ,则1和2是方程
,则1和2是方程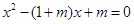 的两个根,由韦达定理,
的两个根,由韦达定理, 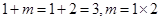 ,所以
,所以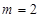 .
.
考点:一元二次不等式、韦达定理

练习册系列答案
相关题目
题目内容
若关于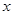 的不等式
的不等式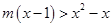 的解集为
的解集为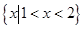 ,则实数
,则实数 的值为 .
的值为 .
2
【解析】
试题分析: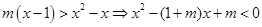 ,解集为
,解集为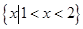 ,则1和2是方程
,则1和2是方程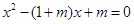 的两个根,由韦达定理,
的两个根,由韦达定理, 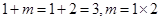 ,所以
,所以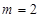 .
.
考点:一元二次不等式、韦达定理
