题目内容
把曲线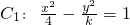 按向量
按向量 =(1,2)平移后得到曲线C2,曲线C2有一条准线方程为x=5,则k的值为________;离心率e为________.
=(1,2)平移后得到曲线C2,曲线C2有一条准线方程为x=5,则k的值为________;离心率e为________.
-3 
分析:把曲线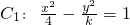 按向量
按向量 =(1,2)平移后得到曲线C2,得曲线C2的中心在(1,2),又因曲线C2有一条准线方程为x=5,故可知曲线C1必为椭圆,结合椭圆的简单性质得到曲线C2的中心到准线x=5的距离为
=(1,2)平移后得到曲线C2,得曲线C2的中心在(1,2),又因曲线C2有一条准线方程为x=5,故可知曲线C1必为椭圆,结合椭圆的简单性质得到曲线C2的中心到准线x=5的距离为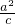 ,据此列出方程式求出c值,进一步求出k和离心率即可.
,据此列出方程式求出c值,进一步求出k和离心率即可.
解答:把曲线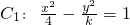 按向量
按向量 =(1,2)平移后得到曲线C2,
=(1,2)平移后得到曲线C2,
得曲线C2的中心在(1,2),
又因曲线C2有一条准线方程为x=5,故可知曲线C1必为椭圆,∴k<0,
此时,曲线C2的中心到准线x=5的距离为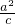 ,
,
即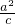 =5-1=4,?
=5-1=4,?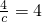 ,?c=1,
,?c=1,
∴-k=a2-c2=4-1=3,?k=-3;
离心率e=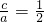 .
.
故答案为:-3; .
.
点评:本小题主要考查函数的图象与图象变化、椭圆的简单性质等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

分析:把曲线
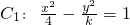 按向量
按向量 =(1,2)平移后得到曲线C2,得曲线C2的中心在(1,2),又因曲线C2有一条准线方程为x=5,故可知曲线C1必为椭圆,结合椭圆的简单性质得到曲线C2的中心到准线x=5的距离为
=(1,2)平移后得到曲线C2,得曲线C2的中心在(1,2),又因曲线C2有一条准线方程为x=5,故可知曲线C1必为椭圆,结合椭圆的简单性质得到曲线C2的中心到准线x=5的距离为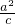 ,据此列出方程式求出c值,进一步求出k和离心率即可.
,据此列出方程式求出c值,进一步求出k和离心率即可.解答:把曲线
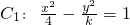 按向量
按向量 =(1,2)平移后得到曲线C2,
=(1,2)平移后得到曲线C2,得曲线C2的中心在(1,2),
又因曲线C2有一条准线方程为x=5,故可知曲线C1必为椭圆,∴k<0,
此时,曲线C2的中心到准线x=5的距离为
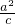 ,
,即
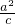 =5-1=4,?
=5-1=4,?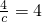 ,?c=1,
,?c=1,∴-k=a2-c2=4-1=3,?k=-3;
离心率e=
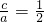 .
.故答案为:-3;
 .
.点评:本小题主要考查函数的图象与图象变化、椭圆的简单性质等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
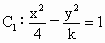 按向量a=(1,2)平移后得到曲线
按向量a=(1,2)平移后得到曲线 ,曲线
,曲线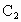 有一条准线方程为x=5,则k的值为________;离心率e为________.
有一条准线方程为x=5,则k的值为________;离心率e为________.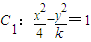 按向量
按向量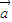 =(1,2)平移后得到曲线C2,曲线C2有一条准线方程为x=5,则k的值为 ;离心率e为 .
=(1,2)平移后得到曲线C2,曲线C2有一条准线方程为x=5,则k的值为 ;离心率e为 .