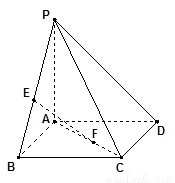题目内容
本题满分16分)
如图,抛物线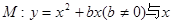 轴交于O,A两点,交直线
轴交于O,A两点,交直线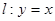 于O,B两点,经过三点O,A,B作圆C。
于O,B两点,经过三点O,A,B作圆C。
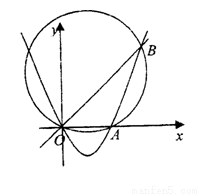
(I)求证:当b变化时,圆C的圆心在一条定直线上;
(II)求证:圆C经过除原点外的一个定点;
(III)是否存在这样的抛物线M,使它的顶点与C的距离不大于圆C的半径?
【答案】
解:(I)易得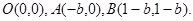
设圆C的方程为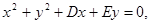
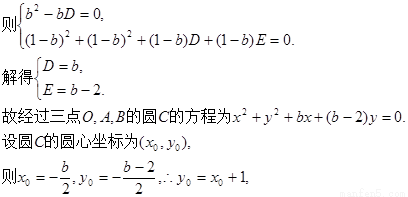 ………………4分
………………4分
这说明当b变化时,(I)中的圆C的圆心在定直线 上。………………6分
上。………………6分
(II)设圆C过定点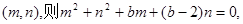
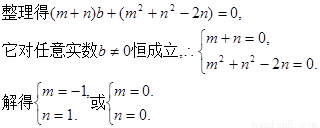 ………………9分
………………9分
故当b变化时,(I)中的圆C经过除原点外的一个定点坐标为(—1,1)。11分
(III)抛物线M的顶点坐标为(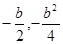 ),若存在这样的抛物线M,使它的顶点与它对应的圆C的圆心之间的距离不大于圆C的半径,
),若存在这样的抛物线M,使它的顶点与它对应的圆C的圆心之间的距离不大于圆C的半径,
则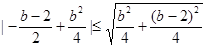 ,………………14分
,………………14分
整理得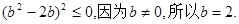
以上过程均可逆,故存在抛物线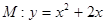 使它的顶点与C的距离不大于圆C的半径。 ………………16分
使它的顶点与C的距离不大于圆C的半径。 ………………16分
【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 所在平面与正
所在平面与正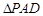 所在平面互相垂直,
所在平面互相垂直,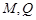 分别为
分别为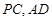 的中点.
的中点.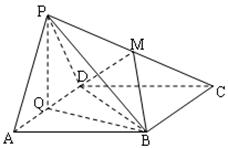
 -
- 的体积;
的体积; 平面
平面 ;
;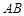 上是否存在一点
上是否存在一点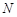 ,使得平面
,使得平面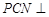 平面
平面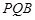 ?若存在,试指出点
?若存在,试指出点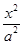 +
+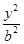 =1(a>b>0)的焦点F1,F2和短轴的一个端点A构成等边三角形,
=1(a>b>0)的焦点F1,F2和短轴的一个端点A构成等边三角形,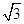 ,
,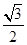 )在椭圆C上,直线l为椭圆C的左准线.
)在椭圆C上,直线l为椭圆C的左准线.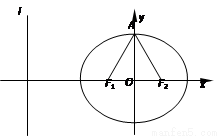
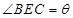 ,试将此人按上述路线从A到C所需时间T表示为
,试将此人按上述路线从A到C所需时间T表示为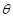 的函数;并求自变量
的函数;并求自变量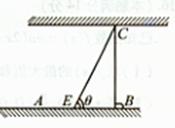
 中,底面
中,底面 是矩形.已知
是矩形.已知 .
.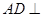 平面
平面 ;
; 与
与 所成的角的大小;
所成的角的大小; 的大小.
的大小.
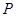 是正方形
是正方形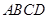 所在平面外一点,
所在平面外一点,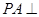 平面
平面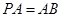 ,点
,点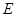 、
、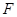 分别在线段
分别在线段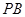 、
、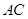 上,满足
上,满足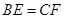 .
.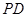 与平面
与平面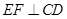 ;
;