题目内容
在棱长为2 的正方体ABCD-A1B1C1D1 中,E 、F 分别为A1D1和CC1的中点.
(1) 求证:EF∥平面ACD1 ;
(2) 求异面直线EF 与AB 所成的角的余弦值;
(3) 在棱BB1上是否存在一点P ,使得二面角P-AC-B 的大小为30°。
(2) 求异面直线EF 与AB 所成的角的余弦值;
(3) 在棱BB1上是否存在一点P ,使得二面角P-AC-B 的大小为30°。
解:如图,分别以DA、DC、DD1所在的直线为z轴、y轴、z轴建立空间直角坐标系Dxyz,
由已知得D(O,0,0)、A(2,0,0)、B(2,2,0)、C(0,2,0)、B,(2,2,2)、E(1,0,2)、F(0,2,1).
(1)证明:易知平面ACD1的一个法向量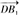 =(2,2,2).
=(2,2,2).
 =(-1,2,-1),
=(-1,2,-1),
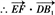 = -2+4-2=0.
= -2+4-2=0.
 ,
,
而EF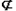 平面ACD1,
平面ACD1,
∴EF∥平面ACD1.
(2)∵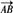 =(0,2,0),
=(0,2,0),
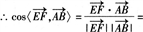

∴异面直线EF与AB所成的角的余弦值为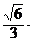
(3)设点P(2,2,f)(0<t≤2),平面ACP的一个法向量为n=(x,y,z),
则
 =(-2,2,0),
=(-2,2,0), =(0,2,t),
=(0,2,t),

取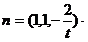 易知平面ABC的一个法向量
易知平面ABC的一个法向量 =(0,0,2),
=(0,0,2),
依题意知 =30°或
=30°或 =150°.
=150°.
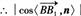
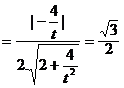 即
即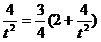 ,
,
解得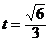
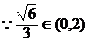 ,
,
∴在棱B,上存在一点P,当BP的长为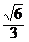 时,二面角P-AC-B的大小为30°.
时,二面角P-AC-B的大小为30°.
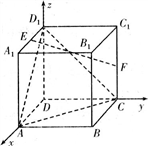
由已知得D(O,0,0)、A(2,0,0)、B(2,2,0)、C(0,2,0)、B,(2,2,2)、E(1,0,2)、F(0,2,1).
(1)证明:易知平面ACD1的一个法向量
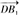 =(2,2,2).
=(2,2,2). =(-1,2,-1),
=(-1,2,-1),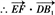 = -2+4-2=0.
= -2+4-2=0. ,
,而EF
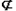 平面ACD1,
平面ACD1,∴EF∥平面ACD1.
(2)∵
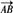 =(0,2,0),
=(0,2,0),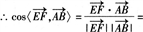

∴异面直线EF与AB所成的角的余弦值为
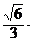
(3)设点P(2,2,f)(0<t≤2),平面ACP的一个法向量为n=(x,y,z),
则

 =(-2,2,0),
=(-2,2,0), =(0,2,t),
=(0,2,t),
取
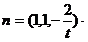 易知平面ABC的一个法向量
易知平面ABC的一个法向量 =(0,0,2),
=(0,0,2), 依题意知
 =30°或
=30°或 =150°.
=150°.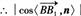
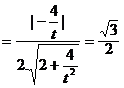 即
即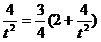 ,
,解得
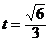
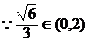 ,
,∴在棱B,上存在一点P,当BP的长为
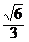 时,二面角P-AC-B的大小为30°.
时,二面角P-AC-B的大小为30°.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
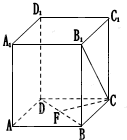 在棱长为2的正方体ABCD-A1B1C1D1中,已知F是线段BD的中点.
在棱长为2的正方体ABCD-A1B1C1D1中,已知F是线段BD的中点.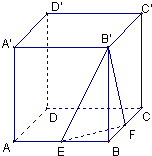 在棱长为2的正方体AC′中,点E,F分别是棱AB,BC的中点,则点C′到平面B′EF的距离是( )
在棱长为2的正方体AC′中,点E,F分别是棱AB,BC的中点,则点C′到平面B′EF的距离是( )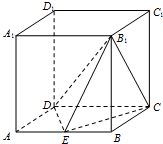 如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为AB的中点.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为AB的中点.